By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
Why peer learning?
Have you ever been on a committee? What about in a study group? Or on a team? Peer-to-peer learning is regularly used in classrooms and workspaces.
When he was CEO of Pixar, Steve Jobs famously transformed the company headquarters. The campus was built on a film’s budget, yet designed with only one bathroom in the atrium. Why?
“If a building doesn’t encourage [collaboration], you’ll lose a lot of innovation and the magic that’s sparked by serendipity. So we designed the building to make people get out of their offices and mingle in the central atrium with people they might not otherwise see.”1
Whether you’re an employee for a multi-billion dollar creative franchise, or a 5th grade student learning about fractions, there is a breadth of research supporting the idea that communication and sharing ideas with your peers leads to deeper learning.
In the last blog post, I spoke about the power behind the Math Stories curricula, which is a sequence of real-world problems that intentionally builds in rigor. As defined by the Common Core, rigor is a well-balanced tripod in which students pursue:
- conceptual understanding,
- procedural skill and fluency, and
- application of skills in problem-solving.
How does the Math Stories protocol reinforce peer-to-peer learning? How can teachers facilitate effective peer learning and what are the lasting benefits?
The Math Stories Protocol
During the 20-minute Math Stories protocol, students deep dive into a story problem connected to a key mathematical concept. Within the Math Stories protocol…

Within this sequence, students model and solve a story problem independently before engaging in a turn-and-talk with a partner to explain their reasoning. This process differs from collaborative learning, wherein a partnership or group of students solve a problem together. By retelling the story problem and using a model to justify how they solved, students are engaging in peer-to-peer learning.
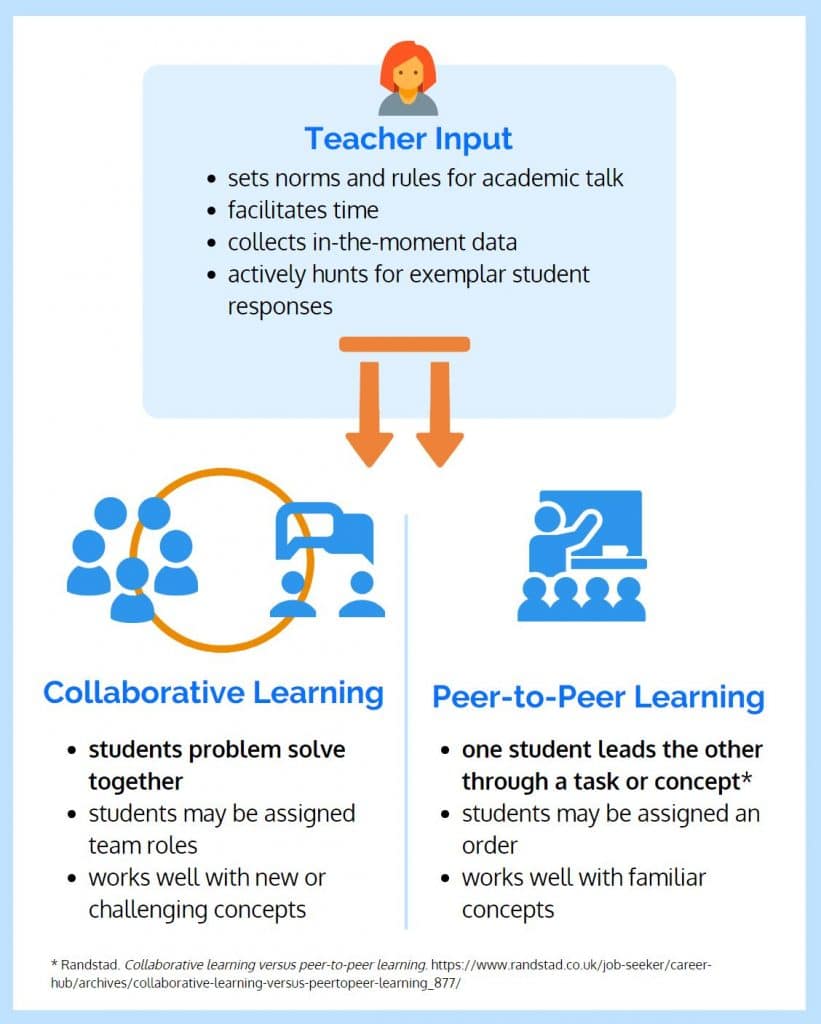
Peer-to-Peer Learning in Action
Let’s consider the following story problem:
Mary and her 5 friends want to split 3 brownies evenly. What fraction of a brownie should each friend get?
Student 1 and Student 2 solve independently using different models to represent their thinking…
Student 1
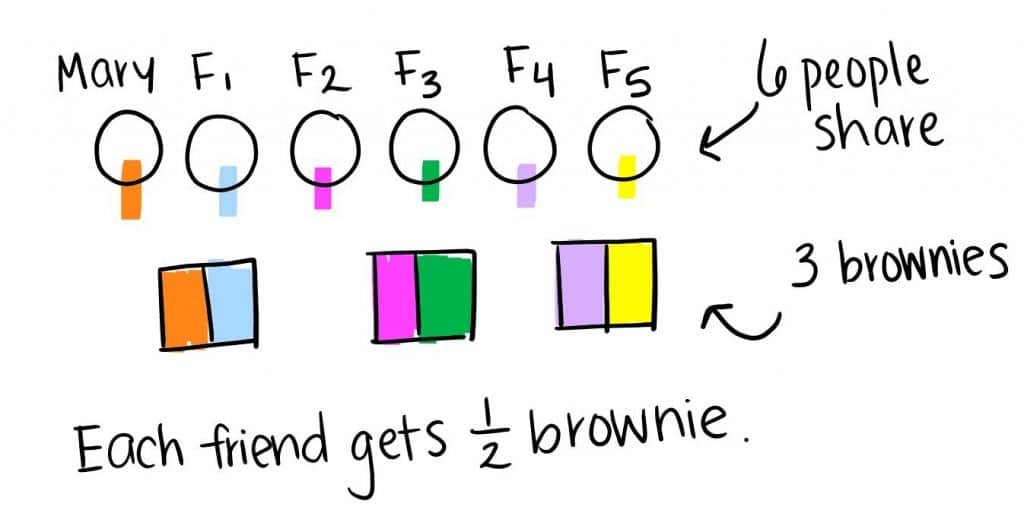 Strategy: Student draws the 6 people sharing (Mary and her 5 friends). By dividing each brownie in half, the student creates 6 equal pieces. Each of the 6 friends get ½ of a brownie.
Strategy: Student draws the 6 people sharing (Mary and her 5 friends). By dividing each brownie in half, the student creates 6 equal pieces. Each of the 6 friends get ½ of a brownie.
Student 2
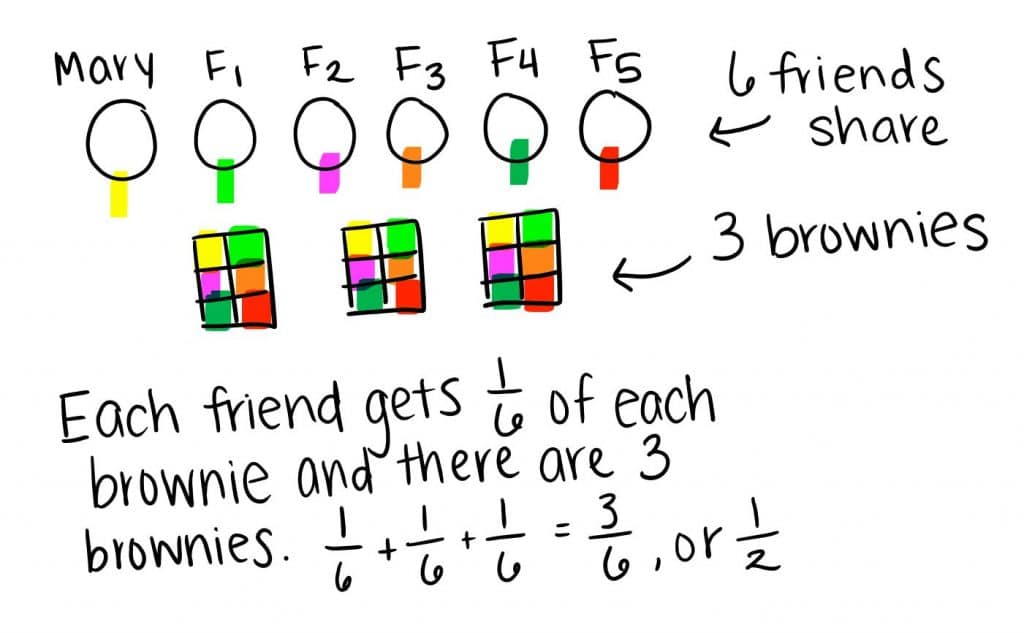
Strategy: Student draws the 6 people. Student partitions each brownie into 6 equal parts, or sixths. Student repeats this process for each brownie and adds the sixths, resulting in each friend getting 3 sixths, 3/6 or ½ of a brownie.
What is the benefit of Student 1 and Student 2 comparing strategies?
Student 1 may have used number sense to intuitively visualize that cutting the 3 brownies in half would generate twice as many pieces to share–the same number as Mary and her friends. This kind of reasoning is powerful and how we want students to be visualizing and making sense of story problems.
Student 2’s strategy of partitioning each brownie by the number of individuals and repeating this process to replicate the number of brownies in the story problem, 3, is messier than Student 1, but it’s a method that’s transferable to more complex numbers. In other words, we can use this strategy no matter the amount of brownies or number of individuals who are sharing.
By engaging in a turn-and-talk, Student 1 and Student 2 each learn a new approach to solving the same problem, as well as practice communicating their reasoning to a peer using mathematical language. Here’s how Student 1 and Student 2 may explain their respective approaches:
Student 1: First, I drew Mary and her 5 friends because those are the people in the story problem. Next, I drew the 3 brownies because it says they split 3 brownies equally. By looking at my drawing, I noticed that if the 6 people were divided into pairs, they’d each share 1 brownie. So, I split each brownie in half. Each friend should get ½ brownie.
Student 2: First, I drew Mary and her 5 friends because those are the people in the story problem. There are 6 people. Then I drew the three brownies. I started with the first brownie and split it into 6 equal pieces, or sixths. Each person gets ⅙ brownie. I still had 2 brownies left, so I split the second brownie into sixths and then the third brownie into sixths. ⅙ + ⅙ + ⅙ = 3/6, which is equivalent to ½ .
Most paramount, is that by teaching one another how they approached the problem, Student 1 and Student 2 are forced to question if and how they are both correct.
A Discussion that Deepens Understanding
As students are retelling the story problem and justifying their reasoning with a partner, the teacher is hunting for student work that he or she can highlight for the discussion. If the teacher sees that almost the entire class solved correctly, they may choose Student 1 and Student 2 to explain their respective approaches to the class and ask:
How are these approaches different?
Students engage in a second turn-and-talk. The discussion question forces students to reread the story problem and reason from the perspective of their peer with the support of a provided visual. There’s increased buy-in because the model being discussed came from a student, rather than the teacher.
In terms of Mary’s brownies, the key concept the teacher is driving students to discover by comparing different approaches is:
Student 1 split each brownie in half, and Student 2 shared each brownie among the 6 friends. Student 1 says each friend gets ½ brownie. Student 2 says each friend gets ⅙ of each brownie, and there are 3 brownies, so each friend gets 3 sixths. ⅙ + ⅙ + ⅙ is 3/6, or ½. They got the same answer even though Student 1 divided and Student 2 used repeated addition.
Shown visually:
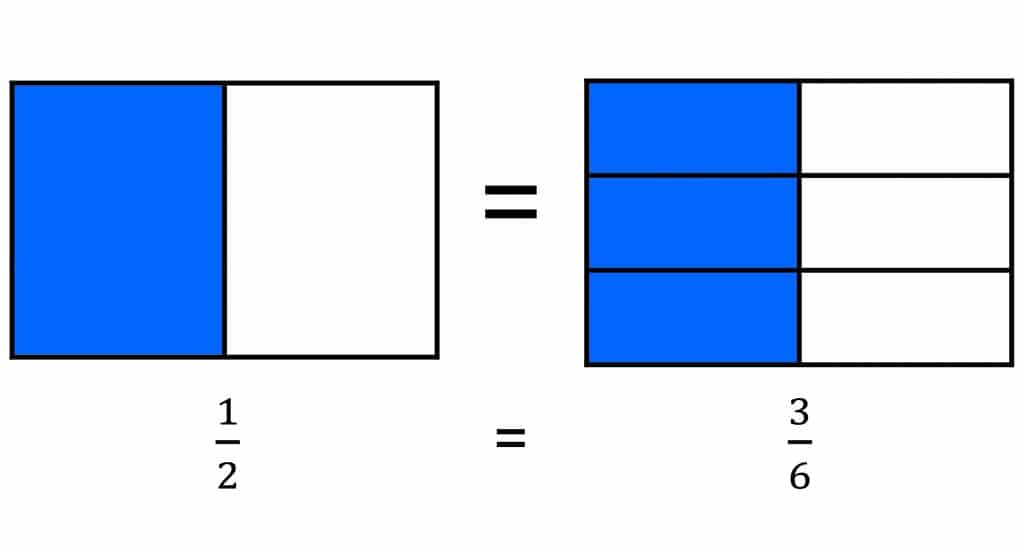
By reasoning if and how both student representations can be correct, scholars are making sense of equivalent fractions in the context of sharing.
It’s important to note that the most learning happens when students are intentionally paired in mixed-ability groups by academic skills, language needs, social dynamics, and behavior (Van de Walle, et al. 2008). Students with differing strengths are more adept at helping one another. For example, an English language learner benefits from being paired with a student who is using mathematical language with precision.
Peer-to-Peer Learning in the Standards
Peer learning is a vital access point for skills within the NCTM Process Standards and the CCSS Mathematical Practice Standards.2 The reasoning and proof standard requires students to critique the reasoning of others, and the communication standard asks students to justify their reasoning to construct a viable argument.

Mary’s brownie problem is an Equal Sharing problem. The Institute of Educational Sciences (IES) recommends using equal sharing activities to develop conceptual understanding of fractions.
According to researchers: “The Common Core State Standards call for partitioning circles and rectangles into equal shares in first and second grade. Therefore, it would make sense that equal sharing problems are a part of instruction in primary grade levels. However, it’s just as important to use Equal Sharing problems with older students to refine and deepen their understanding of fractions (Empson & Levi, 2011).”3
Too often students mistake fractions as separate from whole numbers, rather than quantities on a number line privy to the same mathematical operations. Equal Sharing problems build conceptual understanding by using a relatable context.
What does the research say?
Researchers point to peer-to-peer learning in mathematics as beneficial for a multitude of reasons.
Students…
- practice communication skills and precise language,
- experience reduced classroom anxiety,
- see their teacher cares about their thought process, and
- exercise greater perseverance regarding challenging problems.
When students learn in expectation of teaching others, it actually alters the learning process “promoting greater effort to select the relevant elements and organize them into a meaningful representation” (Benware and Deci, 1984).4 When students are teaching one another, it commands a higher level of understanding.
Researcher John Hattie has spent two decades studying the effect of a multitude of education characteristics– factors like phonics instruction, teacher credibility, and school size. In the most recent ranking, Hattie has combined over a thousand meta-studies concerning a quarter billion students to determine what matters the most to student success. It’s evident from this snippet of his analysis (see chart) that strategies like collaborative group learning and peer tutoring generate a great amount of student progress at little cost.5 For instance, the effect size of peer tutoring is twice that of reducing class size to less than 20 students, an intervention that’s five times more expensive for schools.

Further, when teachers facilitate students teaching one another, they have more flexibility to collect in-the-moment data and listen in on the turn and talks. This leads to more frequent and precise student feedback, which Hattie’s research identifies has a huge effect on a student’s academic success.
Resources
1 Pixar Headquarters and the Legacy of Steve Jobs.
2 NCTM. The Common Core State Standards for Mathematics.
3 Introducing Fractions Through Context with Emphasis on Common Core Progressions. (2014)
4 Laal and Ghodsi. Benefits of Collaborative Learning. (2011)
5 The Economist. Teaching the teachers. (2016)
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


