By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
New Math
“That’s not the way we do it at school, Dad.”
Over the past decade, parents and children on either side of the roll out of Common Core have been having some frustrating conversations about math homework. How can math “change?”

Copyright Pixar, Incredibles 2
In my last blog post, I spoke about effective data collection within Math Stories and how BVP uses interim assessments to track standards-based student growth. But, what exactly is Math Stories assessing? How has international benchmarking and big data changed the professional development of math teachers in the U.S.?
How did we get here?
In the early 2000s, the reauthorization of ESEA as No Child Left Behind transformed the scale of education data available to researchers in the United States. It’s arguable whether the school-accountability tied to NCLB actually caused an increase in student achievement, but it certainly guided researchers and educators to reconsider how we’re teaching mathematics and literacy in American classrooms and examine international competitors with better student outcomes. Compared to the U.S., top-performing countries like Singapore and Japan have rigorous, coherent standards, with tightly aligned instructional materials.1
In 2008, under former Arizona Governor Janet Napolitano, a task force released a report called Benchmarking for Success, which set the groundwork for the Common Core initiative. Shortly after, under the Obama administration, states were incentivized with Race to the Top funds to adopt Common Core.
The sentiment of the movement behind international benchmarking and states adopting Common Core is well captured in the words of OECD leader Andreas Schleicher:
It is only through benchmarking that countries can understand relative strengths and weaknesses of their education system and identify best practices and ways forward. The world is indifferent to tradition and past reputations, unforgiving of frailty and ignorant of custom or practice. Success will go to those individuals and countries which are swift to adapt, slow to complain, and open to change.
In the present skills-driven global economy, there is a heightened demand for a workforce adept at problem solving and using technology. This demand is too pressing, and our students’ outcomes too precious, to dismiss new approaches to teaching math with: but we’ve always done it this way.
Research shows that a conceptual understanding of fractions lays the groundwork for accessing algebra and higher math. BVP has intentionally adopted Math Stories in 5th grade classrooms in addition to their core math block to focus on building conceptual understanding of fractions through story problems.
During Math Stories, teachers follow a 20-minute protocol that puts the heavy lifting on students. The nature of the problem-of-the-day sequence is that students are often exposed to scenarios before they’re explicitly taught in core lessons. This challenges students to make sense of problems by visualizing what is happening and creating a representation that supports their solve strategy. Within this student-centered structure, the teacher collects in-the-moment data about how students are solving and facilitates a discussion in response to real time noticings.
In a traditional banking system of education, the teacher introduces a problem type or strategy and students replicate his or her thinking. In Math Stories, students are free to represent and solve in a number of different ways because as humans we think in a number of different ways. Students create personalized work representative of their conceptual thought process that they can authentically share with their peers and use to justify their reasoning.
What the Data Says
What exactly do we glean about American math students and pedagogy from participating in international assessments like PISA?
Schleicher notes a common trend among American high schoolers in layman’s terms: “Students are often good at answering the first layer of a problem in the United States. But as soon as students have to go deeper and answer the more complex part of a problem, they have difficulties.”2
In familiar and straightforward situations, students are generally able to use algorithms and rote strategies, but they’re less competent when asked to apply mathematical thinking to a non-routine problem in a real life context. Further, they tend to give up on challenging problems rather than try alternate strategies.

This is an alarming trend given that problem-solving in the real world is rarely straightforward or easy.
How can math teachers encourage students to think deeply and conceptually rather than rely on algorithms? How do we build student stamina for complex work?
An Example in Action
Let’s consider the following story problem:
James is 5 ½ feet tall and grows another ¾ foot. How tall is James now?
For most of us, an equation comes to mind first. Students could solve using an algorithm:
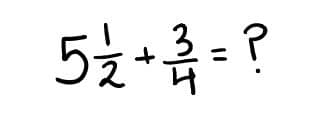
But, if a student doesn’t have the knowledge that we need same units to add and subtract numbers, it may result in the following misconception:
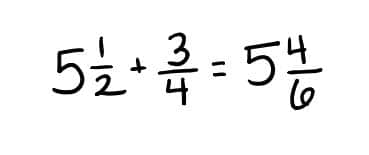
Alternatively, they may know that we can rewrite numbers with equivalent fractions to get the same units, but be at a loss as to how to find the equivalent fraction of ½ without a model.
When they set up an equation or algorithm, students are limited by what knowledge they have. Learners can easily become frustrated and hit a dead end if the problem is not straightforward. However, in Math Stories, students are taught how to visualize what’s happening in the story problem and generate a visual model, which they can use as a tool for finding the solution.
Instead let’s consider two students asked to visualize and model James’ story problem:
Student 1 imagines each foot in James’ height as a separate tape diagram. They imagine five tapes entirely shaded, a sixth tape that is half-shaded, and a seventh tape that is ¾ shaded.
They use a discrete fraction model to represent the whole and partial equations. They partition ½ to make the equivalent fraction 2/4. They combine 5 2/4 + ¾ for a total of 6 ¼ feet.
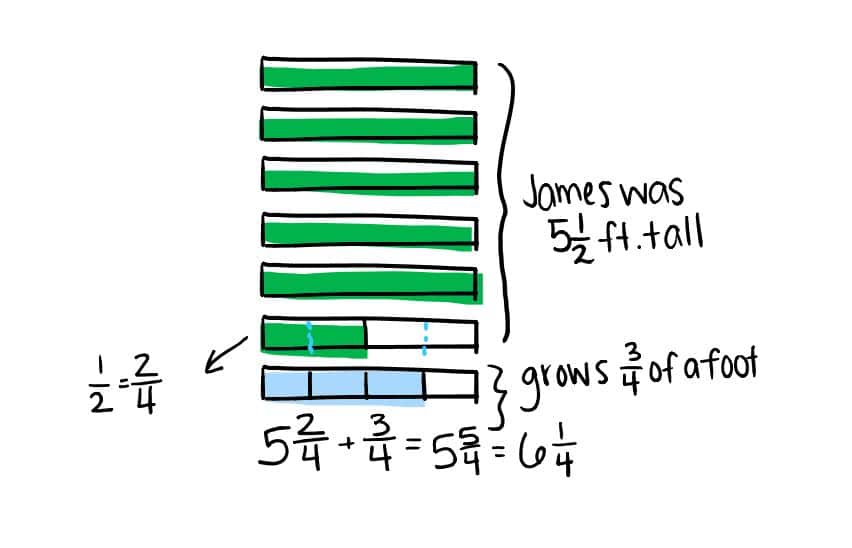
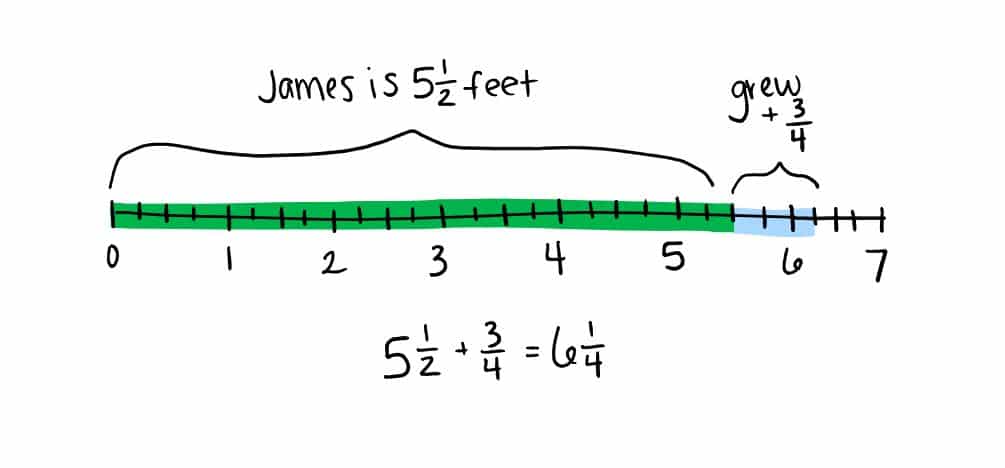
Student 2 imagines James’ height as a line that is 5 ½ feet long. How tall James is now is the endpoint when we add ¾ to his height.
They use a number line partitioned in fourths to represent the whole and partial equations. They recognize that the end point is the total, or how tall James is now.
Both students represented their thinking visually to obtain what is more than a correct answer, but rather a solution that makes sense to them. Through turn-and-talks and discussion, students are able to share this varying work to expand how their peers think.
Peer-to-Peer Learning
During Math Stories, students share their visual model with a partner and use mathematical language to justify their reasoning. Then during the discussion, students engage in a second turn-and-talk about a peer’s chosen strategy. The visual model isn’t only a tool for helping students solve. Models also support students as they explain their thought process aloud. There is a large body of research that points to the power of peer-to-peer learning.
Researcher David Boud reminds us that teachers are tremendously important, but part of their role is preparing students for a world where they engage with public information and the guidance of their colleagues rather than a formal class with a professor.
“The skill of obtaining accurate information is not learned by being given accurate information by a teacher but through practice in discerning how to judge the accuracy of the information we receive.”
Peer-to-peer learning is powerful because it creates students who are able to articulate their thinking and criticize the strategies of others.
What BVP Teachers Say
Teachers at BVP prepare for teaching Math Stories by doing the story problems themselves beforehand to anticipate multiple student solve strategies and possible misconceptions. Don’t be fooled; peer-to-peer learning and student-led discussions do not mean that the teacher is off duty. Teachers have to have a strong understanding of the problem types and models to be able to notice trends in student work during a lesson and identify what needs to be highlighted or revisited. But, BVP faculty are reaping the benefits of investing in the Math Stories framework.
When asked about the impact of the problem-solving instructional block, teachers noted changes in student attitudes and achievement.
Ms. Palumbo at Middle School 1 says, “It is interesting to notice that some of the scholars get really excited when they have to solve problems, and we have noticed decreased anxiety as a whole around word problems. Math stories have also helped with our culture of error and understanding how making mistakes can also be an opportunity for learning.”
Ms. Casali, a teacher at Middle School 2, is noticing similar changes in student attitudes towards mathematics. “I have seen Math Stories support students in becoming better problem-solvers because of the exposure to the amount of word problems they receive…I believe it has shaped their perception in math into a subject that can apply to various parts of their lives. They see where they would use the math they are learning and it makes them more engaged.”
BVP is excited to see the long term impact of building mathematical problem solving skills alongside computation and fluency.
Resources
1 National Governors Association, Council of Chief State School Officers, and Achieve, Inc. (2008) Benchmarking for Success: Ensuring U.S. Students Receive a World-Class Education.
2 Richmond, Emily. The Atlantic. (2016) How do American Students Compare to Their International Peers?
3 Boud, et al. (2014) Peer Learning in Higher Education: Learning from and with Each Other.
Image copyright of Pixar, The Incredibles 2.
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


