By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
Why story problems?
Evan uses ⅔ cup of pineapple for each smoothie he makes. How many cups of pineapple does Evan use to make 6 smoothies?
A snail travels ½ inch every minute. How many minutes will it take the snail to travel 5 inches?
Edna is making trail mix. She adds ⅝ cups peanuts, 2/8 cups raisins and ½ cup almonds. How many cups of trail mix will she make in all?
All of the questions above are examples of fraction story problems. Units about teaching fractions are full of food servings, garden plots, and yards of ribbon. Why?
In my last blog post, I spoke about the impact on student learning when teachers intentionally hunt for student responses during a turn-and-talk to facilitate a meaningful discussion, rather than call on students randomly and hope for the best. This week we take a step back to examine the power behind the actual story problems students are solving during Math Stories.
How does solving story problems support students in building conceptual and procedural skills? What should educators sweat when it comes to teaching story problems?
A Scope and Sequence that Builds in Rigor
During Math Stories, teachers facilitate a 20-minute protocol in which students deep dive into a story problem connected to a key mathematical concept. Within the Math Stories protocol…

The Math Stories scope and sequence is made up of 70 story problems, several sets that include 10-13 problems a month. This allows teachers the flexibility to respond to classroom data and repeat problem types on which students need to spend more time. For the 5th grade fraction story problems, the beginning of the school year focuses on problem types from the previous grade.1 We reloop fraction story problems from the previous grade so that scholars do not lose their fraction learning. In 5th grade, many curricula (like Engage NY) do not teach fractions until the third unit. By focusing on 4th grade fraction story problems at the beginning of the year, we ensure that scholars are ready to engage with rigorous, grade-level story problems as soon as possible.
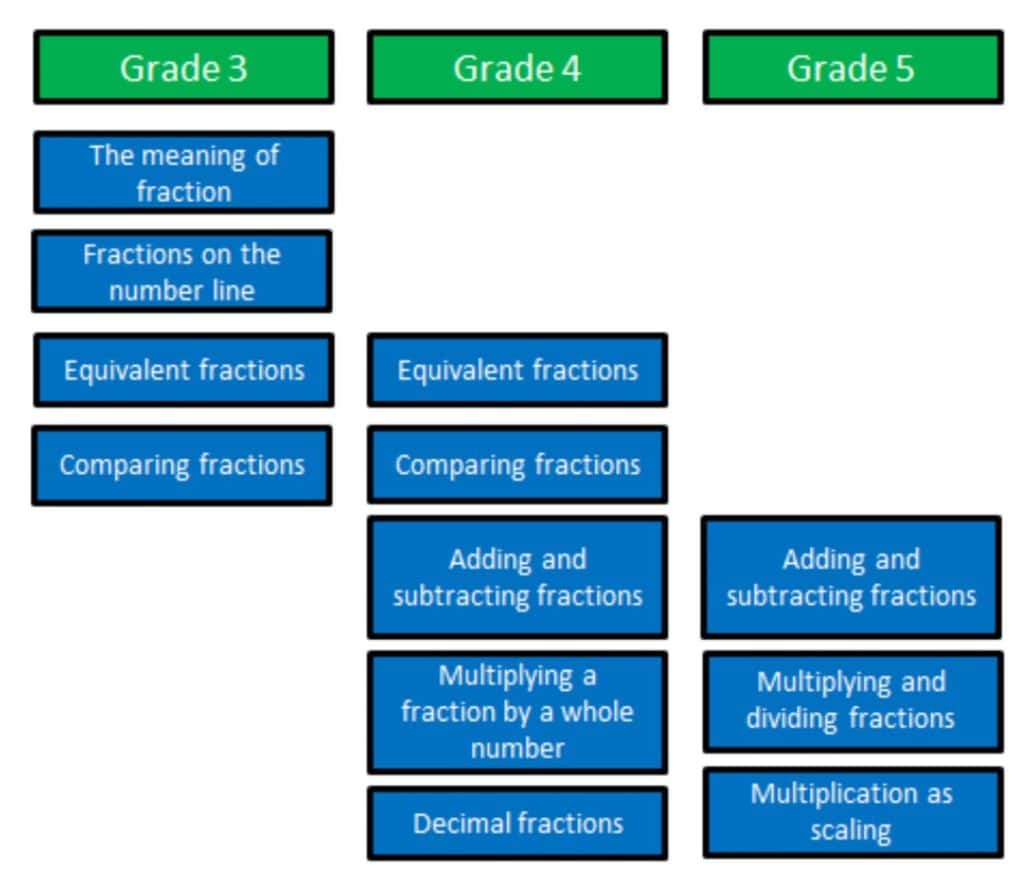
The problem sets intentionally build in rigor. For example, students solve problems with common units for 1-2 months before unlike denominators are introduced. Initially, unlike denominators are restricted to halves, fourths, and eighths and students are only transforming one fraction. This scaffolding allows students to practice partitioning with familiar units and to make sense of equivalency with visual models instead of algorithms.
Students are exposed to halves, fourths, and eighths beginning in 3rd grade, and these familiar units are easier to partition. Additionally, using a model to rewrite one fraction is an evidence-based approach that allows students to develop a real understanding of what an equivalent fraction is and its utility in adding or subtracting unlike units.2
The nature of the scaffolded problem sets is that students are using models to apply new concepts before they’re explicitly taught in core lessons. This creates a powerful classroom dynamic in which the teacher is a facilitator rather than lecturer and students have agency. Researcher John Van De Walle suggests that:
A common teacher misconception is that conceptual understanding of adding and subtracting fractions must precede their work with application. Rather, conceptual understanding and application work together as students leverage real life reasoning to question if and why their representations and answers make sense.
Many teachers believe that scholars cannot learn something until it is explicitly taught. We believe that with the right structures and supports during Math Stories, students can develop creative models and solutions to challenging problems without explicit instruction. Further, when scholars are the agents of their own discovery-based learning, it’s more likely that what they’ve learned is “sticky.” In other words, they’ll remember how and why they approached problem types the way they did and apply this knowledge moving forward.
How the Common Core Defines Rigor
Through international comparisons and analysis of performance on TIMSS, Common Core has identified three shifts in mathematics to increase college and career-readiness among American students:
- Focus: Focus strongly where the Standards focus
- Coherence: Think across grades and link to major topics within grades
- Rigor: In major topics, pursue conceptual understanding, procedural skill and fluency, and application
Rigor as defined by the Common Core does not mean harder. Rigor in math is a well balanced tripod wherein each area requires equal intensity in time, activities, and resources3 :
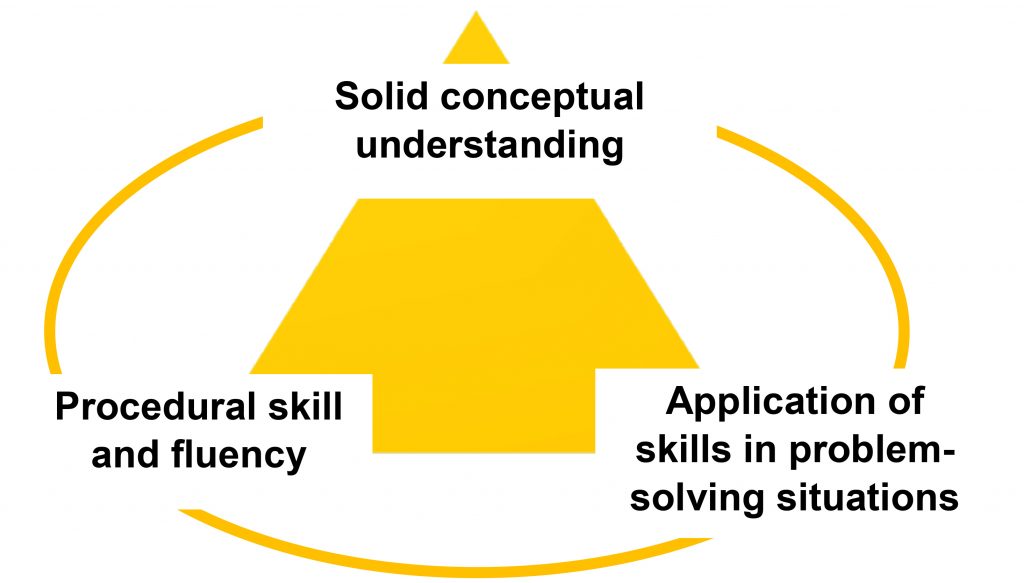
When students are solving story problems in Math Stories, they are flexing cognitive muscles in each of these areas. Students are making meaning of mathematical skills by applying them to real-world situations, such as finding common denominators to add ingredients in a recipe. Story problems enable deeper conceptual understanding by granting students access to a variety of approaches rather than a rote procedure because the teacher chooses examples of student work to discuss as part of the protocol. Finally, the standards provide grade-appropriate fluency benchmarks. Students practice core functions (e.g. add/subtract within 1,000,000 and multi-digit multiplication) during a different instruction time or as homework. A student’s speed and accuracy becomes an asset for manipulating and understanding more complex concepts when they are solving a story problem during Math Stories.
Heads or Tails? One way to supplement story problems
We know that story problems matter. So, what can educators do when they encounter students who are skim reading story problems rather than thinking critically?
While we believe in using the Math Stories protocol to increase scholars’ ability to conceptually understand and solve story problems, we also recognize that there are other strong problem-solving approaches.
The National Council of Teachers of Mathematics (NCTM) and many math coaches suggest utilizing headless and tailless story problems to encourage students to think deeply about the language, context, and structure of a single problem.
Consider the following story problem from Math Stories:
The Tompkins family owns a farm. Their property is 2 1/2 miles wide and 4 1/2 miles long. What is the total area of their land in square miles?
A tailless story problem is one that is missing a question. Here it is written as a tailless story problem:
The Tompkins family owns a farm. Their property is 2 ½ miles wide and 4½ miles long.
Students work in partnerships or groups to record what they know and do not know and generate possible questions. Possible student-generated questions:
- What is the total area of the farm?
- How much longer is the farm than it is wide?
- If the Tompkins family wants 16 square miles of farmland, what are some new possible dimensions?
A headless story problem is one that gives as little information as possible. This is the headless story problem:
The Tompkins family owns a farm. What is the total area of their land in square miles?
Possible teacher prompts:
- Do we have enough information to answer the question?
- What information do we need?
- If I told you that the Tompkins farm is 2 ½ miles wide, would this be enough information? Why or why not?
Students work in partnerships or groups to discuss the information that is given and what information is needed to solve the problem. Without numbers, students cannot jump to plugging numbers into an equation. They must discuss the context, language, and structure of the problem. One benefit of this is it supports students in recognizing patterns among problem types over time.
Headless and tailless story problems emulate the hands-off math that we see in the real world. Mathematics coordinator Tim McCaffrey describes headless tasks as how the world really works. “We start with a question that we wonder about, and we have to go out and search for relevant information.”
Research has shown that connecting mathematics to the real world increases student motivation and understanding, as well as prepares them for work spaces that require mathematical literacy.
Many of us grew up in classrooms that prided quick computation and fact fluency. Have you ever taken a “Mad Minute” quiz? Although fluency is still important, it’s only one leg of the tripod. Exercises in deep diving into real-world problems are key to reminding students that mathematicians are critical thinkers and problem solvers–not calculators.
Resources
1 Illustrative Mathematics.
2 Van de Walle, John et al. (2013) Elementary and Middle School Mathematics: Teaching Developmentally.
3 Achieve the Core. (2016) Introduction to the Math Shifts.
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


