Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
Cometiendo errores
¿Cómo se siente cuando se comete un error?
Hacer sus mejillas al ras? ¿Se siente un peso en la boca del estómago? Quieres rendirte?
La palabra neurológica para esta respuesta es ERN o negatividad relacionada con los errores, y es cómo el cerebro sinapsis fuego cuando se comete un error o no una tarea. Por suerte, Nuestros cerebros (y los cerebros de todos los primates) También están equipados con una respuesta positividad relacionada con los errores, o en, que sigue rápidamente cuando promulgado. Pe nos impulsa a procesar, monitor, y corregir los errores en lugar de aceptar la derrota.1
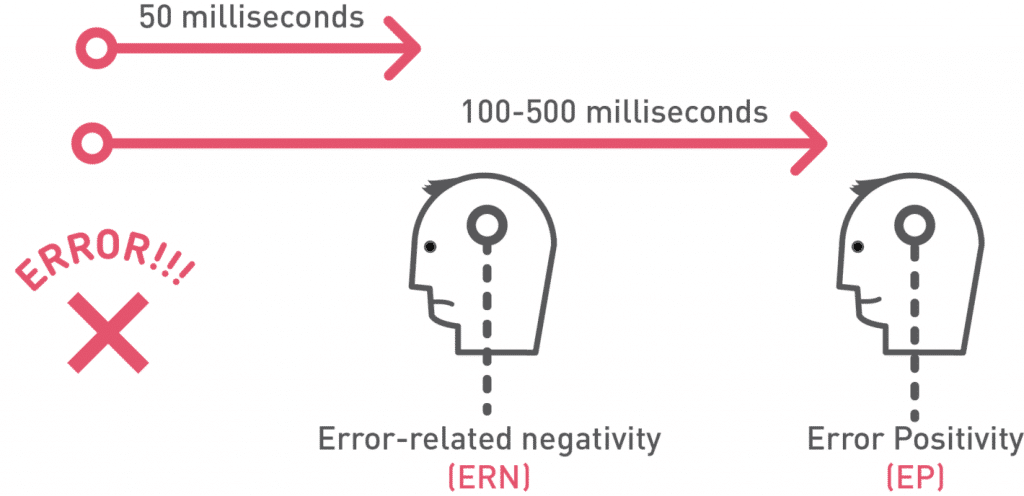 2
2
Lo que es más convincente acerca de los hallazgos neurológicos de otros investigadores del siglo 21 Moser y es que la amplitud de la de una persona ERN y Pe es maleable. En otras palabras, la forma de responder al fracaso es una habilidad que se puede cultivar.
dos modos de pensar
“Tanto si piensas que puedes o no puedes pensar–tienes razón." – Henry Ford
La idea de que podemos fortalecer y hacer crecer el ERN y los receptores de Pe se alinea estrechamente con la investigación psicológica sobre el crecimiento y la mentalidad fijos. psicólogo de la Universidad de Stanford Carol Dweck estudió miles de estudiantes de más de tres décadas para responder preguntas acerca de cómo las actitudes y creencias hacia el aprendizaje afectan el logro. En la base de sus conclusiones es la existencia de dos formas de pensar de aprendizaje polares. Una mentalidad fija percibe la inteligencia como algo estático, mientras que una mentalidad de crecimiento percibe la inteligencia como desarrollado.
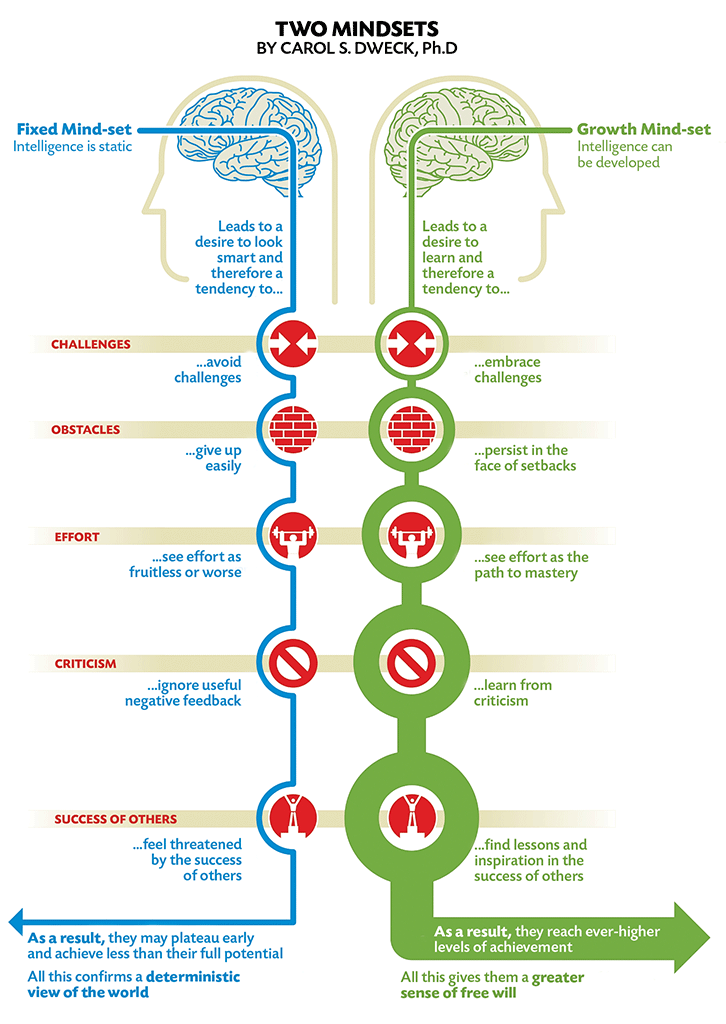
Cuando los maestros y administradores trabajan activamente para cultivar una cultura mentalidad de crecimiento, los estudiantes a ver los errores como oportunidades para aprender más que un reflejo de la frustración de su propia capacidad innata, o la incapacidad. Es importante que los maestros hablen con sus estudiantes sobre la necesidad de la lucha en matemáticas. Cuando es desafiado el cerebro, crece–literalmente.
Un ejemplo en Acción
Historias de matemáticas tiene un protocolo específico para responder a las concepciones erróneas de los estudiantes.
Consideremos el siguiente problema historia:
3 amigos quieren hacer una carrera de relevos de 4 millas. Cada uno de ellos tenga que ejecutar la misma cantidad. ¿Cuántas millas debe ejecutar cada amigo?
Estudiante 1 y Estudiantes 2 resolver de forma independiente utilizando diferentes modelos para representar su pensamiento…
Estudiante 1
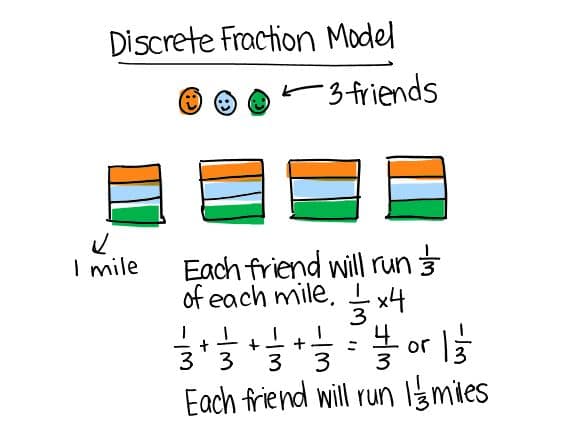
Estrategia:
Estudiante dibuja y denomina a los tres amigos. Se basan cuatro cajas para representar las cuatro millas. Ellos particionan cada milla en tres partes, porque cada uno de los tres amigos corrieron la misma cantidad. ⅓ + ⅓ + ⅓ + ⅓ = 4/3 o 1 ⅓. Cada amigo corrió 1 ⅓ millas.
Estudiante 2
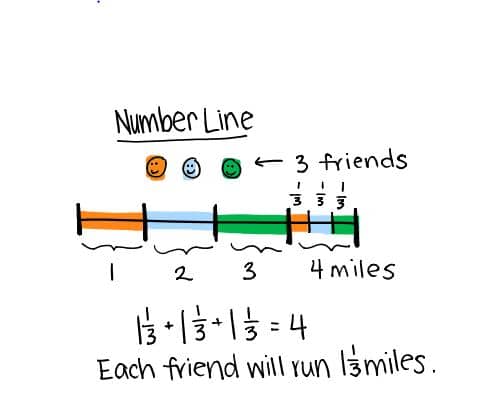
Estrategia:
Estudiante dibuja y denomina a los tres amigos. Se dibujan una línea de números que se extiende a 4 para representar a la 4 millas. Cada amigo corre la misma cantidad de millas, por lo que cada amigo puede ejecutar 1 más millas algunos. Estudiante divide la milla restante en tercios. Cada amigo corre 1 ⅓ millas.
UN Malentendido común es que los estudiantes vayan a revertir la operación…
Estudiante 3

Estrategia:
Estudiante divide el número de amigos, 3, por el número de millas, 4. Cada amigo corre ¾ millas.
Mientras que los estudiantes están resolviendo, El profesor es el seguimiento de forma agresiva. Usando un rastreador de datos, el profesor registra cómo los estudiantes individuales son la solución y se puede medir rápidamente el porcentaje de la clase modela y resuelve correctamente. Si más de la mitad de los modelos de clase y resuelve de forma incorrecta, el protocolo Historias de Matemáticas guía a los profesores para dirigir una discusión acerca de la idea errónea de.
En el ejemplo del problema carrera de relevos, si más de la mitad de la clase incorrectamente modelos ¾ como la solución, el profesor mostrará el trabajo del estudiante con la solución correcta, 1 ⅓, junto con el trabajo del alumno modelar el error, ¾ , y hacer la siguiente pregunta a su vez-y-habla: ¿Cuál de estas soluciones es razonable? Por qué?
¿Cuál es la ventaja de tener la clase de error hablar del Estudiante 3?
Razonando con una idea equivocada
Al discutir si 1 ⅓ o ¾ es una solución razonable con una pareja, los estudiantes están flexionando importantes habilidades de razonamiento y comunicación. Una posible respuesta ejemplar que los maestros cazan para resaltar en la discusión puede ser:
Estudiante 3 dividido el número de amigos, 3, por el número de millas, 4. Cada amigo corre ¾ millas. Esto no puede ser correcto porque sabemos del problema historia que el número de amigos (3), es menor que el número de millas (4). Asi que, sabemos que cada amigo tendrá que ejecutar Más de una milla para conseguir un total de 4 millas. ¾ es demasiado pequeño para ser razonable.
Mediante la evaluación de la validez de error de 3 Estudiante, los estudiantes están revisando el idioma del problema y visualizando el contexto para estimar una respuesta. Este es el tipo de construcción de sentido que queremos que los estudiantes ejercen no sólo durante Historias de matemáticas, pero en todas las aplicaciones de la vida real.
El cultivo de una cultura de riesgo positivo
Este tipo de discusión impulsada por auténticos errores sólo es posible en una clase donde los estudiantes tienen una mentalidad de crecimiento y los errores son una vía hacia la educación superior.
Los maestros están constantemente enviar a los estudiantes que se hablan y mensajes tácitos acerca de su capacidad de aprender. Investigador Jo Boaler sugiere que los maestros presten mayor atención a cómo se están comunicando una mentalidad de crecimiento a los estudiantes en las siguientes áreas:
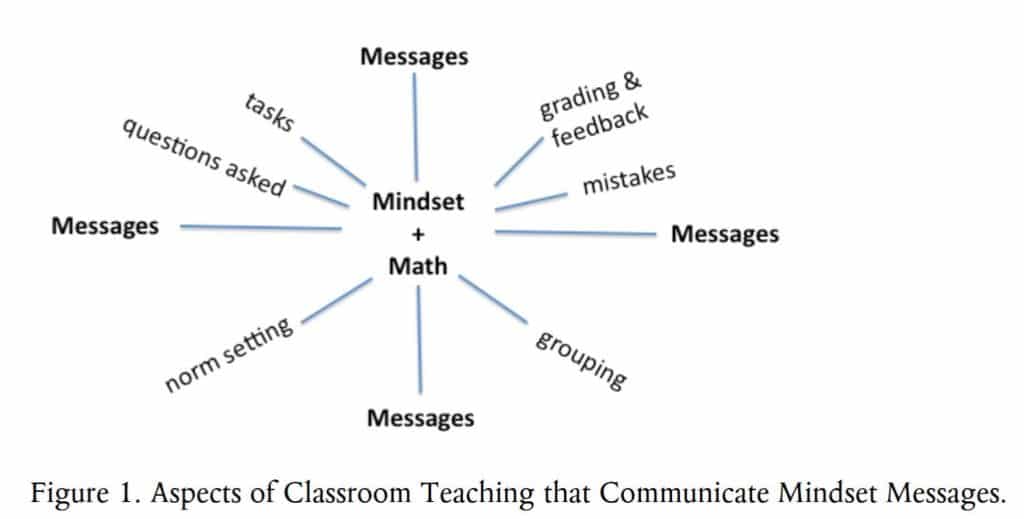
Podemos utilizar dominios basados en la evidencia de Boaler para generar una lista de recomendaciones para enseñar a los estudiantes a ver las matemáticas con una mentalidad de crecimiento:
- Dar a los estudiantes la oportunidad de luchar con largo, problemas difíciles de la historia.
- Establecer normas con los estudiantes por nombrar explícitamente los errores como oportunidades de crecimiento.
- Recompensa la perseverancia y la arena en lugar de “inteligencia”.
- los estudiantes en lugar heterogéneos grupos de habilidad mixta.
- Enseñar a los estudiantes plasticidad cerebral y celebrar el crecimiento en lugar de grados.
- Pedir a los estudiantes a justificar su razonamiento, tanto cuando son correctas e incorrectas.
La investigación de Boaler sugiere que es importante que los maestros piden a los estudiantes para justificar su razonamiento, incluso cuando están correctos. Este hábito enseña a los estudiantes a reflexionar sobre su solución y el sentido de decisiones práctica de forma independiente– no como un reflejo cuando se descubre un error.
Los errores son oportunidades para aprender y pensar profundamente. En lugar de la clasificación con una x roja punitivo, Boaler sugiere incluso se puede tratar una estrella. Antes de utilizar el trabajo del estudiante para resaltar un error, pedir permiso al investigador y dar a conocer que va a ayudar a crecer a toda la clase.
Los estudiantes obtienen mejores resultados cuando tienen conversaciones explícitas con sus maestros acerca de la perseverancia y la importancia de cometer errores. Centro de Investigación de Stanford SIONALES clase Dojo y colaboraron para crear una serie de animación de vídeo 5-parte llamada El Mojo Mostrar para educadores y padres para enseñar a los estudiantes jóvenes sobre la mentalidad de crecimiento. Es una herramienta gratuita con preguntas y actividades de discusión relacionados.
Otra de las principales conclusiones del Boaler es que las prácticas de agrupación perpetúan la creencia mentalidad fija entre los profesores y estudiantes. Los estudiantes son colocados en grupos basados en la capacidad con una mayor prevalencia en la U.S. e Inglaterra en comparación con los países de alto rendimiento como Japón y China. Promover, muchas investigaciones han demostrado que aunque los profesores creen que están dando más trabajo “adecuada” a los estudiantes colocados en los grupos de bajos, que a menudo no es lo suficientemente exigente (Blatchford et al.). Los estudiantes pueden estar recibiendo clases de recuperación o “doble inmersión” durante una hora diferente del día para llenar los vacíos académicos, Pero las historias de matemáticas es una oportunidad para que los estudiantes aprendan de sus errores y para lograr altos niveles ... porque poder.
recursos
1 Moser, y. Alabama. (2011) Cuida tus errores: La evidencia de un mecanismo neuronal vincular el crecimiento mentalidad para ajustes de adaptación Posterror.
2 Caviglioli, Oliver. (2015) errores.
3 Boaler, ya.La Matemática de la Esperanza: Pasar de rendimiento para el aprendizaje en clases de matemáticas.
4 Tax et al. Un clima de error constructiva como un elemento del ambiente de aprendizaje efectivo.
5 Boaler, ya. (2013) Capacidad y Matemáticas: la revolución mentalidad que está transformando la educación.
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani


