Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
No deje al azar
Cómo tomar decisiones importantes? ¿Se lanza una moneda? Consulte a un confidente? ¿Qué pasa con el uso de la recopilación de datos con propósito?
Al entrar en Blackstone Valley Prep durante Historias de matemáticas y que no verá la maestra en la parte delantera de la sala de dar una conferencia. En lugar, La señorita Palumbo da instrucciones a toda prisa y estudiantes empezar a esbozar modelos matemáticos que representan su pensamiento. Unos minutos más tarde, se establece un temporizador bajo el retroproyector y el zumbido de diálogo académico llena la habitación como académicos a su vez a un socio para explicar su modelo y justificar su razonamiento. Ella no está interviniendo o señalar errores. Ella está ocupada seguimiento de forma agresiva, mirando el trabajo del estudiante. En lugar de centrarse en el cumplimiento o el uso de una lista de verificación simplemente para marcar si un estudiante resuelve el problema correctamente, maestros están utilizando un rastreador de datos para registrar las estrategias específicas y conceptos erróneos que ven en el trabajo del estudiante.
En la última semana de entrada en el blog, Hablé acerca de la importancia de la asignación de asociaciones intencionales-habilidades mixtas exponer a los estudiantes a nuevas estrategias y reforzar el vocabulario matemático. Como estudiantes de modelo y luego girar-y-habla en asociaciones, qué datos es el maestro recogiendo? ¿Cómo informar a la recogida de datos en-el-momento de enseñanza y aprendizaje?
Un espectro de trabajo del estudiante
Las Historias de matemáticas protocolo incluye una plantilla de preparación intelectual. Para cada problema de palabras, maestros preparan mediante la búsqueda de la solución a sí mismos. registran:
- La gran idea / puntos clave,
- una gama de modelos de estudiantes ejemplares anticipados,
- posibles conceptos erróneos,
- preguntas para la discusión sobre la base de los estudiantes’ comprensión, y
- respuestas de destino.
Este proceso ayuda a los maestros a internalizar objetivos de matemáticas y estrategias para la historia específica de matemáticas. Cuando los maestros son fluidos en los conceptos matemáticos, ellos pueden dedicar más energía a la vigilancia para entender y toma de decisiones críticas.
Consideremos el siguiente problema historia:
bebidas janae 7/8 de un litro de agua. bebidas Javon 1/2 un litro de agua. ¿Cómo beber Janae mucha más agua que Javon?
Visual:
Algunos estudiantes imaginar dos jarras de agua de tamaño cuarto de galón. jarra de janae se divide en 8 a partes iguales, y ella bebe 7 octavos. jarra de Javon se divide en 2 a partes iguales, y bebe 1 mitad. La solución puede ser imaginado como las bebidas extra de agua Janae en comparación con Javon.
Modelo:
UN modelo fracción discreta se utiliza para mostrar la partición. Los diagramas de cinta están alineados de manera uniforme con el fin de comparar dos cantidades y encontrar una fracción equivalente.
Conocimiento:
Los estudiantes usan su conocimiento que cuánto más nos está pidiendo para comparar las cantidades de agua y Janae Javon consumido. En otras palabras, encuentra la diferencia. Pero, no podemos sumar o restar los números a menos que tengamos las mismas unidades. Los estudiantes saben podemos encontrar fracciones equivalentes de 1/2 mediante la partición de un diagrama de cinta. Cortando 1/2 en cuatro partes y luego de nuevo en octavos, es evidente que 1/2 es igual a 4 octavos (4/8). Los estudiantes se alinean los diagramas de cinta y encontrar la diferencia contando la cantidad “extra” de agua que bebió Janae.
Visual:
Algunos estudiantes imaginar una oración numérica substracción. Cuánto más significa que el problema está pidiendo la diferencia entre dos cantidades, en este caso, la cantidad adicional de agua bebidas Janae en comparación con Javon. 7/8 – 1/2= ___.
Modelo:
Los estudiantes representan la información de la historia usando un problema ecuación etiquetada con la fracción equivalente.
Conocimiento:
Los estudiantes utilizan el conocimiento de que para restar fracciones, debemos tener unidades equivalentes. razón por la que los estudiantes 1/2 es una fracción unidad familiar que puede ser transformado más fácilmente que 7/8. 8 es igual a 2 grupos de 4, por lo que una media de 8 Se puede escribir como 4/8. Ahora estamos restando 4 octavos de 7 octavos, cual es 3 octavos (3/8).
Conceptos erróneos
En términos del problema historia Janae y Javon, hay varios errores posibles estudiantes pueden hacer:
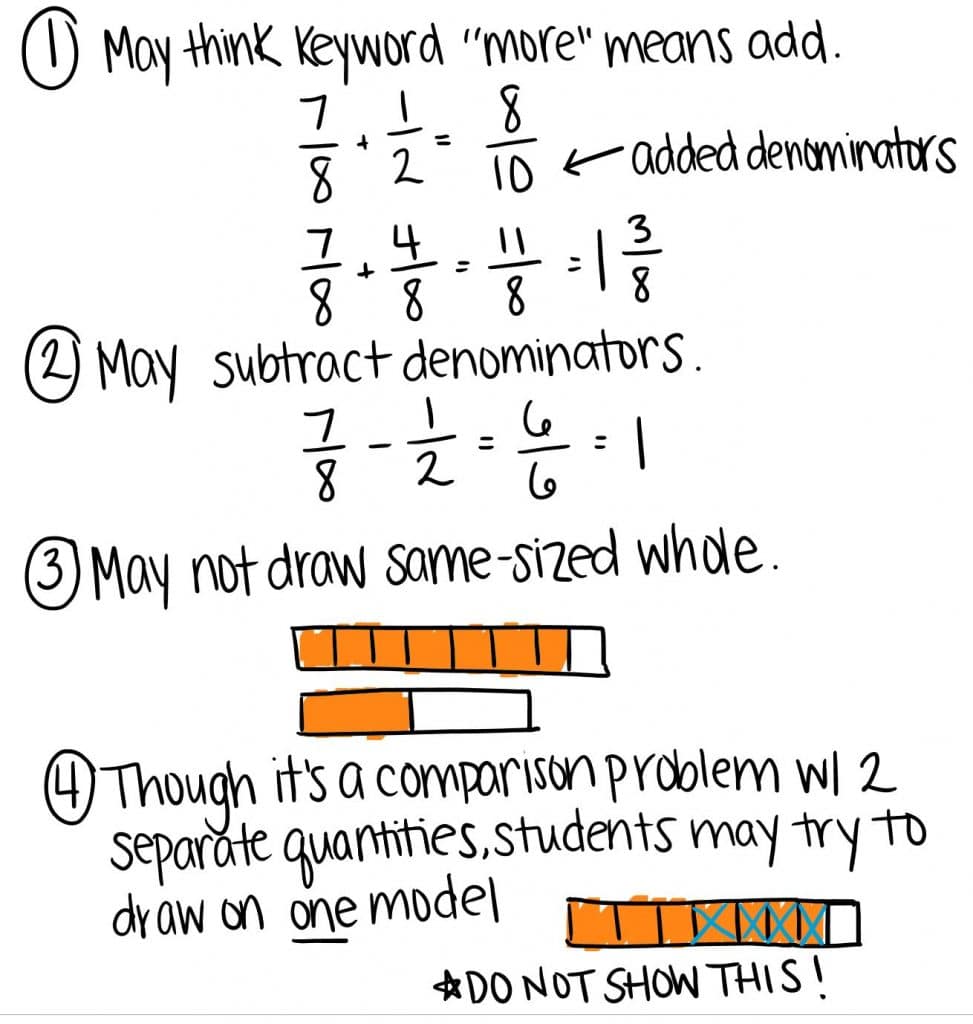
Las ideas falsas son apropiadas para el desarrollo y parte del proceso de aprendizaje. No son errores como mucho, ya que son señales valiosas que un concepto matemático necesita ser revisado. Promover, conceptos erróneos permite que el profesor para facilitar una discusión en la que los estudiantes practiquen justificar su razonamiento y utilizando el vocabulario pertinente.
viendo vs. Monitoreo agresiva
Director General de las Escuelas Poco frecuentes, Proyecto taxonomía y autor de Enseñar como un campeón, Doug Lemov, describe una diferencia clave entre los profesores que miran vs. el seguimiento de los estudiantes de manera agresiva. Aquí es un extracto de Enseñar como un campeón, Guía de campo 2.0:
El legendario entrenador de baloncesto John Wooden, ofreció este consejo a los maestros…: “Nunca confunda la actividad para el logro.” Un gimnasio ocupado con zapatillas de deporte chirridos o una clase llena de lápices de rascarse es evidencia de actividad. Esto es a menudo una buena cosa, pero diferente y más fácil de detectar que logro un gimnasio o una sala de clase que produce estudiantes que pasan y se mueven o ecuaciones del factor de forma impecable.
monitoreo agresivo se centra en el aprendizaje más que la gestión, y Lemov sugiere realizar un seguimiento de los maestros dos indicadores clave: errores específicos y puntos de éxito. Como parte del protocolo, maestros predeterminan lo que el trabajo del estudiante debe ser similar a la calidad, así como trampas impacientes, y el propósito de la vigilancia agresiva es para los maestros observen patrones de trabajo de los estudiantes para saber cómo ajustar su enseñanza en respuesta. Adicionalmente, la investigación con las Escuelas Poco frecuentes sugiere que los mensajes de monitorización agresivos a los estudiantes que se valora su esfuerzo y la calidad de sus asuntos de trabajo.2
El uso de un rastreador de datos
Como se ha mencionado más arriba, un principio clave de historias de matemáticas está monitoreando de manera agresiva mientras que el modelo estudiantes y vuelva a contar el problema historia y explicar su modelo de representación a un socio. Usando un rastreador de datos, el profesor registra cómo los estudiantes individuales son la solución y se puede medir rápidamente el porcentaje de la clase modela y resuelve correctamente. Hay tres maneras de responder a datos de los estudiantes en función de la calidad del trabajo del estudiante:
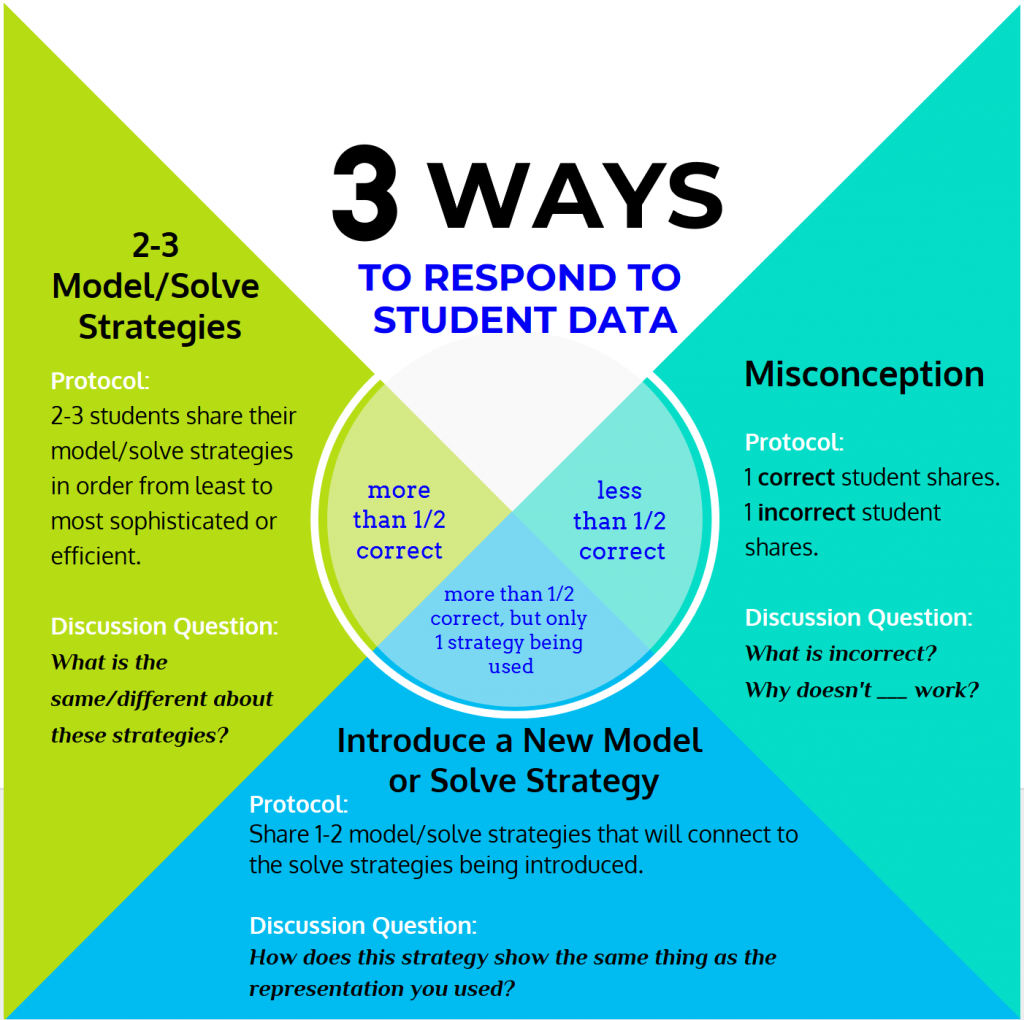
¿Cómo se ve esto como en un aula durante Historias de matemáticas?
Ejemplo 1
Rastreador de datos:
![]()
Podemos ver en los datos de seguimiento del maestro que un poco más de la mitad de la clase resuelto correctamente. Tres estudiantes utilizaron un modelo de fracción discreta correctamente y dos utilizaron una ecuación marcado correctamente.
Protocolo: El profesor elige al menos dos estudiantes para compartir, uno con un modelo de fracción discreta y una con una ecuación marcado. Al discutir cómo estas dos estrategias son representan la misma idea, los estudiantes están expuestos a diferentes enfoques y empujaron a compararlos para la eficiencia.
Pregunta de discusión: Lo que es igual / diferente acerca de estas estrategias?
Ejemplo 2
Rastreador de datos:
![]()
Podemos ver en el rastreador de datos que un tercio de la clase resuelto correctamente, y una mayoría de estudiantes compartió la idea errónea de que el lenguaje “cuánto más” en el problema de la historia nos está pidiendo que añadir.
Protocolo: El profesor elige un estudiante que añade de forma incorrecta y un estudiante que modela la búsqueda de la diferencia para facilitar una discusión en torno a la idea errónea de desenmascarar. Al tener que justificar su razonamiento usando el contexto de Janae y Javon, los estudiantes a entender mejor “cuánto más” y las diferencias conceptuales entre las operaciones.
Pregunta de discusión: ¿Qué modelo representa con exactitud la historia?
Ejemplo 3
Rastreador de datos:
![]()
Podemos ver en el rastreador de datos que la mayoría de la clase resuelto correctamente, pero los estudiantes sólo se utiliza un modelo de fracción discreta para resolver.
Protocolo: En este caso, el profesor utilizará el modelo del estudiante para guiar a los estudiantes a escribir la ecuación correspondiente etiquetado.
El profesor puede introducir el modelo diciendo: “Vi a un estudiante el año pasado ...” o “Un estudiante en otra clase ...” para mantener dirigida por los estudiantes aprendiendo incluso cuando los conceptos clave están ausentes del estudiante trabajar ese día.
Pregunta de discusión: ¿Cómo muestra esta estrategia lo mismo que la representación que utilizó?
Por qué es importante
La investigación en torno al lenguaje y matemáticas indica que cuando los estudiantes se les enseña habilidades de comunicación, razonando juntos en una discusión de grupo mejora el aprendizaje y la comprensión de los conceptos matemáticos individuo.1 Al evaluar rápidamente el trabajo del estudiante y escuchando a su vez-and-Talk conversaciones, Los profesores pueden elegir preguntas de discusión que tienen más impacto en la comprensión de los estudiantes.
En cada ejemplo data tracker, el profesor utiliza el trabajo real del estudiante para responder a los patrones de clase, en lugar de confiar en una corazonada. Este enfoque garantiza que cada lección está activo–disolver conceptos erróneos, la comparación de una serie de estrategias, y la construcción hacia la eficiencia y modelos más sofisticados. En-el-momento de datos permite a los maestros a los estudiantes se mueven más rápidamente que utilizando sólo las evaluaciones provisionales o tickets de salida.
recursos
1 Mercer, Neil (2006). Enseñar a los niños a usar el lenguaje para resolver problemas matemáticos.
2 Bambrick-Santoyo, Pablo (2016). A mejorar más rápido: Un plan de 90 días para el entrenamiento de nuevos maestros.
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani


