Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana

¿Cuál de estos problemas de matemáticas tiene más sentido para usted?

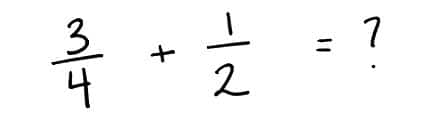
Combinar 3/4 y 1/2.

 

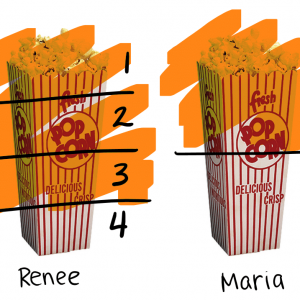
Renee come 3/4 bolsa de palomitas. Entonces María se come 1/2 bolsa de palomitas. La cantidad de palomitas de maíz tenían Renee y María comen por completo?

 

Ambos problemas requieren la misma habilidad–encontrar fracciones equivalentes para combinar dos números con distinto denominador. Pero, la cuestión de palomitas de maíz proporciona un realista contexto para que.

“La enseñanza a través resolución de problemas puede ser descrito como boca abajo de la enseñanza para la resolución de problemas, el problema(s) presentado en el comienzo de la lección y las habilidades que salen de trabajar con el problema(s).”¹

La estructura narrativa de la pregunta problema historia invita a los estudiantes a crear un modelo con etiquetas. Dentro de un modelo fracción discreta, particionan los estudiantes para encontrar la fracción equivalente:

 

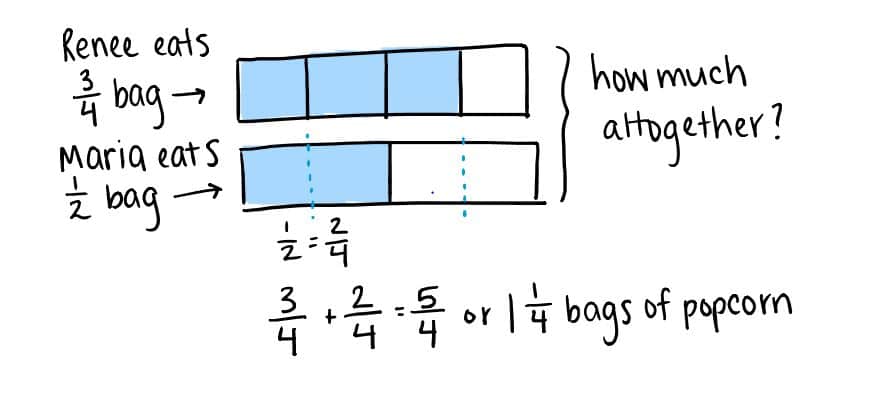
Dentro de un número de modelo line, la historia de palomitas de maíz se visualiza de forma más explícita como una serie de eventos, el último salto a la suma:

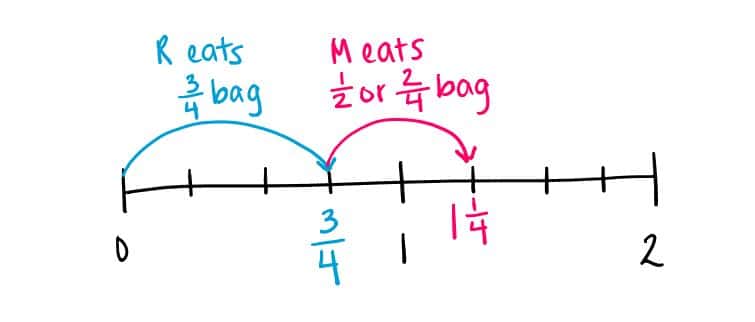
Mediante la creación de un modelo para combinar las porciones de palomitas de maíz, los estudiantes son guiados para descubrir el procedimiento para encontrar fracciones equivalentes. Promover, inmediatamente se conocen un contexto realista, donde una habilidad matemática se puede aplicar, y los estudiantes pueden observar más fácilmente en los patrones de los tipos de problemas que utilizan estrategias más eficientes y resolver escenarios cada vez más complejos.

 

El Aula Basado en Problemas

en un 2006 entrevista conversacional, profesor de matemáticas y autor John A. Van de Walle hizo hincapié en la necesidad de que todas las aulas estadounidenses a una norma enfoque basado en problemas conducido por las ideas de los estudiantes en lugar de la conferencia dirigida por el maestro. Cuando el maestro está dando una conferencia en un enfoque de mostrar y contar, Van de Walle argumenta que los estudiantes se centran en las instrucciones y reglas en lugar de los conceptos matemáticos.

Con un basado en problemas abordar el estudiante tiene a quién recurrir aparte de sus propias ideas en relación con el problema. Como resultado, en lugar de buscar reglas, estudiantes intentan dar sentido a las ideas relevantes incrustadas en el problema o tarea. Incluso si una problema no se resuelve, sus propias ideas relevantes han participado. La discusión de la clase que sigue será significativa e interesante. Las ideas son desarrollados e integrados con la comprensión existente de cada alumno.

 

Para mí también es muy importante tener en cuenta lo que cada enfoque está diciendo cada día para los estudiantes. Con dirigido maestro, explicaciones maravillosas, estudiantes a menudo ven las matemáticas como un conjunto de reglas que a menudo se vuelven confusas y tienen poco significado ... En los estudiantes en el aula basados ​​en problemas…experimentar el hecho más básico de las matemáticas: matemáticas tiene sentido. Promover, se dan cuenta de que ellos son los que son capaces de dar sentido a las matemáticas.¹

los 20-minutos protocolo Historias Math es un enfoque centrado en el estudiante que simplemente no lo sugiere Van de Walle–obliga a los estudiantes a tomar de forma independiente sentido de problemas difíciles en contextos realistas. ¿Cómo pueden los maestros contexto de apalancamiento en Historias de matemáticas y durante su bloque central de instrucción? ¿Por qué importa contexto en un enfoque centrado en el estudiante?

No es de rutina resolución de problemas

Parte de la visión de Van de Walle es que las matemáticas no se trata de ser capaz de identificar los tipos de problemas y aplicar algoritmos sencillos. Más bien, la solución de un problema de matemáticas no es habitual.

Las definiciones de la resolución de problemas variar a través de programas de estudio, pero en esencia son preguntas no son de rutina que se pueden resolver utilizando más de una estrategia. “Aprender estrategias múltiples puede ayudar a los estudiantes a ver diferentes ideas y enfoques para la resolución de problemas y pueden permitir a los estudiantes a pensar de manera más flexible cuando se le presenta un problema que no tiene una solución obvia.”

El Math secuencia Historias quinto grado tiene aproximadamente 70 problemas de la historia. Es una progresión cuidadosamente andamiaje que comienza con una revisión de los conceptos de 4º grado, a continuación, un par de meses en, los estudiantes se trasladan a las normas de 5to grado de fracciones utilizando las cuatro operaciones. En general, existen 10-13 problemas de la historia al mes, lo que da a los maestros la flexibilidad en espiral tipos de problemas difíciles y volver a conceptos.

Lo que es clave sobre el problema diario historia es que presenta un desafío matemático en contexto. Proporcionar contexto es crucial para apoyar a los estudiantes en el sentido de decisiones y resolución de problemas flexibles. Promover, problemas de la historia apoyan a los estudiantes en el desarrollo de habilidades en tres áreas RAND (una empresa de investigación enorme nonpartison) ha considerado necesario para la construcción de dominio:

• Representación
• Justificación
• Generalización

 

Apoyar la independencia del estudiante

Mientras que los estudiantes pueden ser preparados para identificar el tipo de problema en una lección explícita y seguir un procedimiento familiar, Historias de Matemáticas, los estudiantes no se les da ninguna información, además del problema de palabras. A medida que van de Walle sugiere, esta estructura de no intervención obliga a los estudiantes a pensar acerca de la información que ya saben y lo que se les pide a resolver para. teóricamente, esto suena muy bien, pero en las aulas los alumnos tienen necesidades diferentes, Todavía se están desarrollando habilidades metacognitivas, y con frecuencia son rápidos en descremada problemas y se basan en algoritmos sencillos.

¿Cómo formar a los estudiantes a leer detenidamente problemas de la historia?

 

la lista de verificación

UN la lista de preguntas puede apoyar a los estudiantes en la lectura de un problema historia de fondo para la información conocida y desconocida. El Centro de Información Qué da resultado (WWC) es financiado por el Instituto de Ciencias de la Educación (IES) a través de la U.S. Departamento de Educación y es un gran recurso de la investigación en educación. Aquí está la lista de muestras de CMA de indicaciones:

 

Modelo de auto monitoreo y Reflexión

Los maestros deben modelar cómo utilizar indicaciones como las mencionadas anteriormente, para razonar con uno mismo todo el proceso de resolución de problemas–cuando se lee el problema historia, la elección de una estrategia para resolver, y verificación del trabajo. Los estudiantes aprenden del ejemplo de la forma de pensar en voz alta a sí mismos cuando se resuelve un problema de palabras. Aquí está un ejemplo de la WWC, adaptado para Historias de matemáticas, de un auto-monitoreo estudiante. El estudiante pregunta y responde a una serie de preguntas que es la misma sin importar el tipo de problema:

 

Ejemplo Problema

5 amigos están pensando en la división 3 pizzas uniformemente. Uno de los amigos no pueden venir a la cena más. ¿Cuánto más de pizza serán los amigos conseguir si sólo se 4 la gente se separaron las pizzas en lugar de 5 La división de la gente pizzas?

Solución*

Estudiante: primero, me pregunto: "Sobre qué es la historia, y ¿qué necesito para averiguar?” Veo que el problema me ha dado la cantidad total de pizza y dos escenarios diferentes para compartir el importe total de la pizza. Sé que “cuánto más” me está pidiendo para comparar, o restar, la diferencia entre la cantidad de pizza cada amigo se mete en cada escenario.

me pregunto, “¿He visto un problema como este antes?” Como pienso en los problemas de la historia que hemos hecho, Recuerdo haber visto un problema donde los amigos compartían una bandeja de brownies. Recuerdo que tuvimos que dividir el todo por el número de amigos para conseguir parte de cada amigo. Este parece ser el mismo tipo de problema, pero voy a tener que dividir en dos ocasiones porque hay dos escenarios y luego comparar.

Antes de continuar, me pregunto, “¿Qué pasos debo seguir para resolver este problema?” Parece que tengo que dividir la cantidad total de la pizza por el número de amigos para cada escenario.

4 amigos: 3/5 la pizza por persona

5 amigos: ¾ de pizza por persona

El problema me está preguntando “¿cuánto más” pizza los amigos reciben cuando sólo hay 4 las personas que dividen en lugar de 5. Yo sé que cuando estoy comparando, o la búsqueda de una diferencia, Puedo utilizar restas. Pero, Tengo que tener las mismas unidades para restar.

Puedo usar mi modelo:

Para escribir una ecuación:

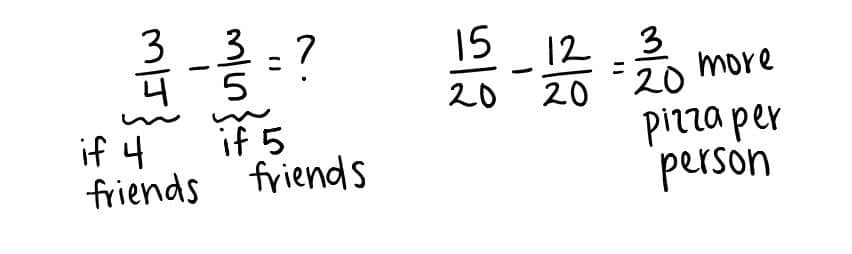
Asi que, la diferencia es 3/20. Los amigos cada uno consiguen 3/20 más pizza cuando sólo hay 4 en comparación con las personas cuando hay 5.

Finalmente, me pregunto, “¿Tiene este sentido la respuesta cuando vuelvo a leer el problema?” Tiene sentido para mí que 3/20 es la respuesta, ya que es la diferencia entre el tamaño de la porción de 5 amigos y 4 amigos. 3/20 es un número pequeño comparado con el tamaño de las porciones. (Lo sé 3/10 es lo mismo que 0.3 o 3%, y 3/20 es incluso menos!) Esto tiene sentido ya que el problema me está pidiendo para encontrar la diferencia-quitando 1 amigo hace una pequeña diferencia en la cantidad de pizza obtendrá cada persona.

 

No están familiarizados con el apoyo de idiomas y contextos

Es cierto que los estudiantes encontrarán idioma desconocido y el contexto en evaluaciones formales que van a tener que lidiar con y sin la ayuda de un maestro o compañeros. sin embargo, como estados WWC: “El objetivo de asegurar que los estudiantes entiendan el lenguaje y el contexto de los problemas no es hacer menos difícil problemas. En lugar, es permitir que los estudiantes se enfocan en las matemáticas en el problema, en lugar de en la necesidad de aprender nuevos conocimientos o lenguaje fondo. El punto principal es que los alumnos deben entender el problema y su contexto antes de intentar resolverlo.”Por esta razón, es importante que los maestros anticipan cuando los estudiantes de 5º grado en su clase pueden necesitar aclaraciones adicionales, especialmente los estudiantes del idioma Inglés. Este es un ejemplo adaptado de WWC usando matemáticas problemas historia historias:

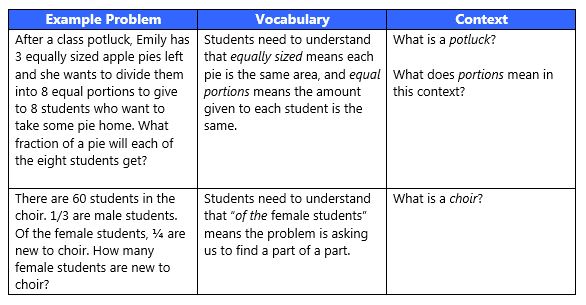
Problemas personalizar historia

WWC y otras investigaciones sugieren estudiantes están más comprometidos y pueden hacer conexiones a las aplicaciones de la vida real de matemáticas cuando se personalizan problemas de la historia. Los maestros deben tener cuidado de no hacer esto todo el tiempo– los estudiantes necesitan para acostumbrarse a pensar en escenarios fuera de su zona de confort. Pero, a veces incluyendo nombres de los estudiantes, tendencias queridos como Beyblades, y que tienen estudiosos vienen con sus propios escenarios, puede aumentar la participación. Cada problema historia en Historias de matemáticas está basado en estándares, por lo que es fácil de intercambiar el contenido para el contenido que es relevante para su salón de clases mientras sigue la enseñanza de conceptos clave.

recursos

¹ (2006) Una conversación con John Van de Walle, autor de primaria e intermedia matemática escolar: Enseñanza Desarrollo.

² RAND. (2003) Competencia matemática de todos los alumnos: Hacia un Programa de Investigación y Desarrollo Estratégico en la Educación Matemática.

 

Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani