Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana

Los profesores de matemáticas Cantando una melodía diferente

 

¿Quién recuerda esta canción o una tecla de acceso similares? Muchas personas se enorgullecen de recordar el procedimiento para dividir fracciones. Si no puede, una rápida búsqueda en Google le proporcionará fórmulas, tablas de anclaje espolvoreado con flechas, e incluso recordar las estrategias de los tradicionales métodos mayoría de los adultos de tres pasos fueron enseñadas como hijos.

Pero, puedes explicar por qué mover de un tirón y se multipliquen se obtiene la respuesta correcta?

Hay consecuencias para el aprendizaje de las matemáticas (como la división de fracciones) como procedimientos de cálculo en lugar de conceptos podemos visualizar, dibujar, y explicar el uno al otro. Cuando los estudiantes no son empujados a utilizar representaciones visuales y explicar su pensamiento, pueden empezar a creer que las matemáticas son procedimientos numéricos sin sentido. Esta frustración se extiende solamente cuando los estudiantes se mueven en el álgebra más abstracto.¹

En el último entrada en el blog, Me ofrecieron consejos para apoyar a los educadores a medida que enseñan fracciones conceptualmente el uso de las normas comunes básicas de matemáticas. Durante su bloque de Historias de Matemáticas, maestros en Blackstone Valley Prep piden a sus investigadores a utilizar modelos de fracciones visuales para representar y resolver problemas de la historia fracción. Pero, lo que está sucediendo fuera de los bloques de instrucción para prepararse para Historias de matemáticas?

 

Los maestros hacen las cuentas

La mayoría de los adultos se les ha enseñado fracciones en la misma forma que estamos tratando de mejorar para nuestros estudiantes. Como profesores de matemáticas, tenemos que cambiar nuestra forma de pensar y cinturón de herramientas antes de que podamos ser los expertos.

Cuando los maestros de 5to grado en la BVP preparan para enseñar una lección Historias de Matemáticas se acerca, primero tienen que entrar en los estudiantes’ mentalidad. Ellos siguen un protocolo de plan de lecciones paso a paso- para modelar el problema de matemáticas historia a sí mismos e internalizar puntos clave.

 

 

Tome este problema de palabras, por ejemplo,:

bebidas Adelaide ½ litro de agua cada día. ¿Cuántos días le tomará para beber 4 litros de agua?

 

Paso 1: Gran idea

Lo primero que nuestros maestros hacen es señalar la gran idea o punto clave(s) en el problema de palabras. Por ejemplo:

• Punto clave 1: modelos fuertes representan lo que está sucediendo en la historia con las etiquetas detalladas.
• KP2: modelos fracciones fuertes ayudan a resolver problemas sin depender del algoritmo.
• KP3: No hay una sola manera “correcta” de pensar en un problema o sólo una “operación apropiada.” (Con la adición agrupación, los niños a menudo se basan en la adición o multiplicación.)

 

Paso 2: representaciones

Siguiente, los maestros a crear 2-3 representaciones anticipan de los estudiantes utilizando etiquetas transparentes. Por ejemplo, El problema de Adelaida podría ser modelado utilizando una modelo fracción discreta, numero de linea, o Además con ramificación:

 

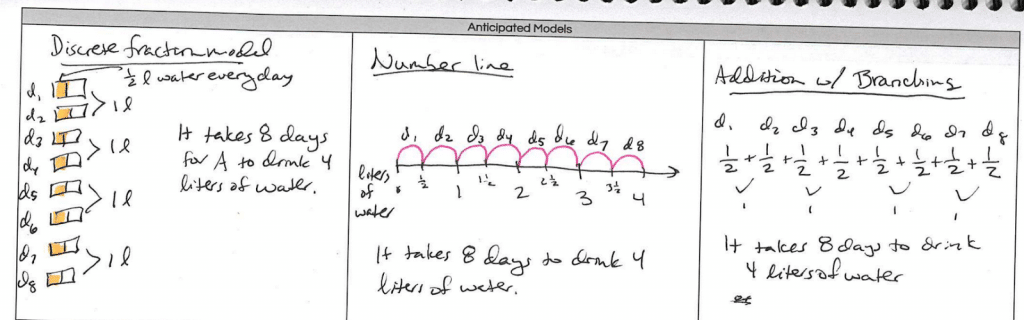
Paso 3: Conceptos erróneos

Entonces, maestros anticipan posibles conceptos erróneos de los estudiantes.

Por ejemplo, en la historia de Adelaida, los estudiantes pueden modelar los números y ½ 4 Del problema, pero incorrectamente asumir la operación. Es importante tener en cuenta con la división de la agrupación que los niños pueden añadir varias veces y media hasta que obtengan una suma de 4, pero se olvidan de las restricciones problema original que nos dan un total de 8 días.

 

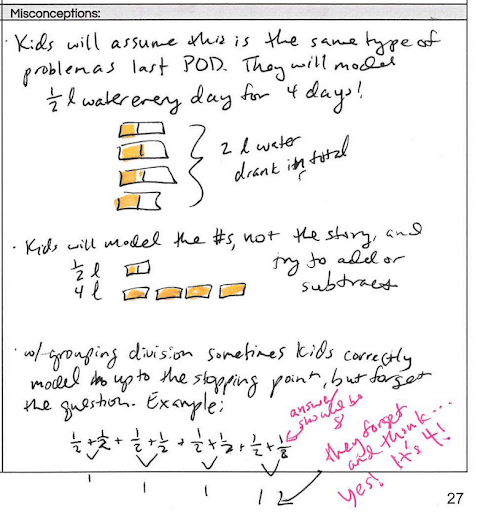
Paso 4: Preguntas y respuestas de discusión Ejemplares

Finalmente, maestros preguntas de discusión pre-plan para tres escenarios posibles que pueden surgir mientras se están controlando los modelos de estudiante. Si mas que 50% de estudiantes son la solución correcta, el profesor facilitará 2-3 estudiantes que comparten sus modelos con la clase utilizando el lenguaje matemático. Para el problema de Adelaida, el maestro tiene previsto elegir 2 modelos ejemplares con etiquetas claras.

Girar y hablar Pregunta de discusión: “¿Cómo podemos usar estos dos modelos para demostrar que se necesita 8 días para beber 4 litros de agua?”

Respuesta de destino: Podemos utilizar los modelos para ver que se necesita 2 días para beber 1 litro, por lo que toma 8 días para beber 4 litros. También pudimos contar con la línea número que 8 litros de medio = 4 litros, por lo que toma 8 días.

El estudiante muestra un pensamiento flexible y utiliza etiquetas para la explicación clara.

haga clic aquí para un ejemplo de un plan de clase completado Historias de matemáticas y aquí para una plantilla en blanco.

 

Vale la pena?

Cuando los problemas de matemáticas maestros modelo en múltiples formas, identificar los puntos clave y preguntas de discusión alineados, y anticipar las ideas falsas como parte de la preparación para problemas de la historia de la fracción enseñanza, que han aumentado la confianza frente a los estudiantes y son más capaces de facilitar una discusión dirigida por los estudiantes.

Promover, cuando el maestro está prevista para los diferentes niveles de comprensión de los alumnos, que son capaces de utilizar los datos en-el momento de facilitar una discusión que satisface las necesidades actuales de los estudiantes y les empuja hacia la comprensión conceptual y dominio de los estándares. Al saber qué buscar durante la aplicación, el profesor puede aprovechar la potencia y la voz de los estudiantes a través de sus modelos en lugar de depender de la conferencia dirigida por el maestro. Este enfoque cultiva una habitación de matemáticos jóvenes que son más propensos a tomar riesgos y se sienten cómodos cometer errores.²

 

Querer aprender más?

En los próximos mensajes, vamos a explorar las diferentes partes del protocolo de Historias de Matemáticas, así como el poder de student.

Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani

 

recursos

1 El desafío de las fracciones, NCTM.

2 dominó. “Las influencias sobre los profesores por actitudes hacia las matemáticas,” 2009.