Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana

Ponga sus lápices de Down!

¿Qué hacer los maestros de 5º grado en Blackstone Valley Prep dicen que es el primer paso para la solución de problemas? “Ponga sus lápices abajo!”

estudiosos de la escuela secundaria en BVP está en el segundo mes de la implementación del protocolo Historias de Matemáticas, que utiliza materiales de Escuelas FirstLine en Nueva Orleans para centrarse en problemas de la historia de fracciones. El bloque de 20 minutos se llama Historias de matemáticas y empuja a los estudiantes a seguir un protocolo estructurado de 3 pasos cada vez que se acercan a un problema de palabras.

En un pasado entrada en el blog, Hablé acerca de la importancia de la enseñanza de las matemáticas como conceptos podemos visualizar, dibujar, y explicar el uno al otro, en lugar de algoritmos como descerebrados. Pero, ¿Cómo funciona exactamente el protocolo Historias de Matemáticas reforzar la visualización y comprensión conceptual?

 

Hacer una película Mente

Consideremos el siguiente problema historia:

Renee come 3/4 de una bolsa de palomitas de maíz. María come 1/2 de una bolsa de palomitas de maíz. La cantidad de palomitas de maíz tenían Renee y María comen por completo?

Eruditos en silencio escanear el problema de palabras como Miss Palumbo lee dos veces. “Lápices abajo,”Ella suavemente les recuerda, animándoles a visualizar lo que está sucediendo en su contexto.

Es útil imaginar Renee y María. Tal vez están sentados en una sala de cine o en frente de un televisor. Hay dos bolsas de palomitas de maíz, y estamos interesados ​​en encontrar al total comido. La visualización de la situación e identificar información conocida y desconocida es un importante primer paso para representar y resolver un problema de palabras. Después de que el problema se lee dos veces, estudiantes en cuenta la pregunta y información en un hoja de registro.

Pero, algo poderoso está sucediendo antes que los estudiantes anoten la información clave. A medida que los estudiantes están escuchando, que están empezando a visualizar un modelo matemático en su sano. Al dibujar esta visualización como una representación, los estudiantes a resolver de una manera que tenga sentido para ellos y puede ser explicado a los demás.

 

Representación de la visualización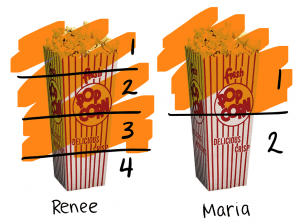

Los estudiantes pueden han visualizado bolsa de palomitas de Renee divide en 4 partes iguales y bolsa de palomitas de María roto en 2 a partes iguales. Antes de utilizar una representación de resolver, estudiantes son particionamiento imaginación y se puede visualizar que las unidades no son los mismos.

esta visualización, o una película mente, ayudará a los estudiantes representan utilizando una modelo claramente etiquetado. La representación ayuda al estudiante a resolver y se utiliza para justificar su razonamiento a un compañero.

Permitiendo a los estudiantes a visualizar un problema y elegir un proceso que tenga sentido para ellos, naturalmente, da lugar a una variedad de enfoques. Este cultiva la confianza a través de un clima de la clase que se preocupa más por la comunicación y habilidades flexibles que “obtener la respuesta correcta.” Los estudiantes se mueven de forma natural a partir de estrategias concretas para más eficiente, métodos abstractos. Cuando los estudiantes se les enseña cómo dibujar modelos que representan lo que están pensando, que están a cargo de su propio aprendizaje. No importa la complejidad del problema, los estudiantes pueden lidiar con las habilidades que tienen en el presente.

En este enfoque centrado en el estudiante, eruditos solidifican la comprensión de los conceptos matemáticos mediante la representación y la solución de problemas de la historia múltiples maneras. Promover, los contratan porque las estrategias son procedentes de sus pares. El papel del maestro es recopilar datos sobre cómo los estudiantes representan, tomar una decisión sobre la cual las representaciones serán compartidos con toda la clase, y facilitar una discusión sobre un punto clave matemática.

 

Modelo discreta Fracción

Visual:

Los estudiantes que se visualizó rompiendo cada bolsa de palomitas de maíz en partes de un todo y la adición de las partes juntas.

Modelo: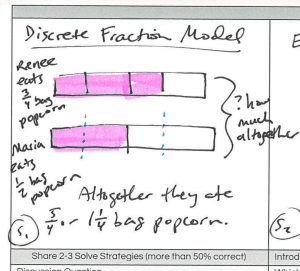

Los estudiantes pueden dibujar una diagrama de cinta para mostrar la iteración o partición.

Objetivo de rendimiento del estudiante:

Sé de suma y resta de números enteros que necesitamos las mismas unidades. He utilizado una estrategia llamada particionamiento y un modelo de diagrama de cintas para mostrar ½ y ² / ₄ son fracciones equivalentes. Mitades y los cuartos son diferentes unidades, pero si vuelvo a escribir como ½ ² / ₄ , Tengo la misma unidad. Puedo añadir ² / ₄ y ¾ Llegar
⁵ / ₄ o 1 ¼.

 

Numero de linea

Visual:

Los estudiantes que visualizó Renee comer casi la totalidad bolsa de palomitas y luego comer un poco de María, pero menos de Renee.

Modelo: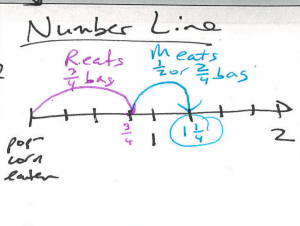

Los estudiantes pueden dibujar una numero de linea para mostrar la iteración o partición.

Objetivo de rendimiento del estudiante:

Sé de suma y resta de números enteros que necesitamos las mismas unidades. He utilizado una estrategia llamada particionamiento y un modelo de línea de números. Empecé dibujando 2 totalidades que representan la 2 bolsas de palomitas. Luego partí los totalidades en 2 partes iguales para hacer mitades y otra vez para hacer cuartas. Solía ​​saltos en la recta numérica para mostrar lo que come Renee, ¾ , además de lo que se come María, ½. El último número es el total, o lo que comían por completo, cual es 1 ¼.

 

El fortalecimiento de habilidades de visualización

¿Cómo se puede mejorar los estudiantes’ capacidad de visualizar problemas de la historia?

Usar una variedad de modelos

Para desarrollar una profunda comprensión conceptual de las fracciones, es importante que los estudiantes utilizar varios modelos para representar el mismo problema historia y aprender nuevas estrategias para la representación de discute el trabajo entre pares.

Conecte fracciones a lo que los estudiantes ya saben sobre los números enteros.

Es importante que los maestros introducen fracciones conectándolos a lo que los estudiantes ya conocen números enteros y continuar haciendo hincapié en esta relación.

Enseñar iterativo Idioma

Muchos adultos están familiarizados con particionamiento, o romper un todo en partes iguales. Piense rebanadas de pizza y gráficos de tarta. sin embargo, tanto la investigación apunta a la importancia de los estudiantes también tienen una punto de vista iterativo. En otras palabras, viendo 3/4 como un contar de tres cuartas partes llamadas.

símbolos de fracciones son sólo una forma abreviada de decir cuántos y qué (Van de Walle et al.).

 

Por qué eso importa?

El protocolo de Matemáticas Historias visualización es un componente crítico que apoya a los estudiantes en la creación de modelos matemáticos significativos. Dibujo y compartir modelos visuales en el contexto mejora el sistema número aproximado de los estudiantes (AÑOS), que se correlaciona con una mejor simbólico-matemáticas, o la capacidad aritmética (Parque & Brannon, 2013). En otras palabras, pensar visualmente no es un sustituto de operaciones simbólicas–es una habilidad indispensable que fortalece nuestra capacidad de pensamiento abstracto.

Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani