Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
Asociarse
¿Alguna vez ha tenido un compañero de laboratorio? Un cónyuge? ¿Qué pasa con un socio a su vez-y-habla?
Al entrar en Blackstone Valley Prep durante Historias de matemáticas y verá estudiantes inclinándose cortésmente y tomar turnos para explicar sus modelos y soluciones matemáticas. ellos asienten, pedir a sus preguntas asociadas, y, a veces expresar confusión. asociaciones con propósito apoyar a los estudiantes, ya que explicar los modelos de representación, articular los conceptos clave, y desarrollar nuevas estrategias para la búsqueda de soluciones a través de un discurso significativo.
En la última semana de entrada en el blog, Hablé acerca de la importancia de los estudiosos la visualización de un problema de palabras en contexto antes de la creación de un modelo que tenga sentido para ellos. Una vez que los estudiantes han representado a su proceso de pensamiento en un modelo claramente etiquetados y resuelto, ¿Cómo pueden los maestros utilizar asociaciones intencionales para construir un diálogo significativo con respecto a los conceptos matemáticos?
Como parte del protocolo Historias Math, los estudiantes escuchan como el problema de la historia se lee 2-3 tiempos y visualizar lo que está sucediendo, representar mediante un modelo que apoya su visualización, y girar-y-habla con un compañero para explicar su razonamiento.

Después 2-3 eruditos presentan su acercamiento a la clase, socios se involucran en un segundo giro y charla para discutir una pregunta elaborada por el maestro abordar el punto clave de la lección.
¿Por qué es este primer giro y charla beneficioso para los estudiantes?
Las representaciones abstractas y concretas
Los estudiantes se acercan a problemas de la historia de diferentes maneras. Es importante que los estudiantes modelo en la forma que tenga más sentido para ellos, porque esto lleva a conversaciones potentes, en lugar de una cultura académica estancada donde los estudiantes son entrenados para representar de la misma manera. Cómo concreto o abstracto proceso de un estudiante se depende:
- cómo ellos visualizado el problema historia
- qué las estrategias que les han enseñado, y
- cómo confidente se sienten ejecutar ciertas habilidades.
Consideremos el siguiente problema historia:
hornea Ellis 9 empanadas. El da 3/4 de un pastel a cada uno de sus 5 amigos. La cantidad de pastel de no haber dejado Ellis?
Visual:
Algunos estudiantes imaginar nueve empanadas cortadas en cuartos. ellos sombra 3 cuartas cinco veces para representar las partes Ellis da a sus amigos. Encuentran el sobrante total contando las cuartas partes sombreadas.
Modelo: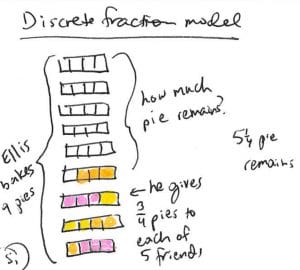
UN modelo fracción discreta se utiliza para mostrar la separación y la iteración.
Conocimiento:
Ellos utilizar su conocimiento de fracciones y las relaciones parte-todo-parte para contar las cuartas partes sombreadas y hacer la conexión que esta es la diferencia, o lo que queda.
Visual:
Algunos estudiantes imaginar una oración numérica substracción. Comienzan con nueve pasteles. ¾ restan cinco veces por cada amigo Ellis da tarta para. La diferencia es la cantidad de pastel de Ellis ha dejado más de.
Modelo: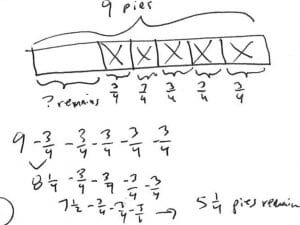
UN diagrama de cinta genérica se utiliza para mostrar la partición. Un ecuación se utiliza para mostrar resta repetida.
Conocimiento:
Ellos utilizar su conocimiento del medio y un cuarto (fracciones de referencia) para restar cinco veces.
Visual:
Algunos estudiantes imaginar una oración numérica substracción. Comienzan con nueve pasteles. Reconocen que restar ¾ cinco veces es el mismo que restar el producto de ¾ * 5 de 9, o 3 ¾ .
Modelo: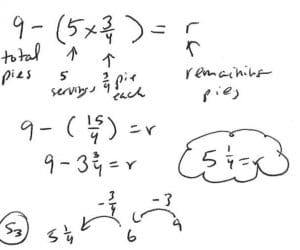
UN ecuación marcado se utiliza para mostrar el número total de las empanadas, 9, y la cantidad dada de distancia (5* ¾).
Conocimiento:
Ellos utilizar su conocimiento que repite la suma / resta es la misma que la multiplicación para escribir la ecuación 9 – (¾ * 5) . Promover, saben que al restar una fracción impropia de un número entero, está más limpia para convertirlo en un número mixto, por lo que puede restar el todo y luego las partes.
Es muy importante que los estudiantes se dan problemas de la historia con operaciones diferentes, contextos, y la complejidad, de manera que se los alienta a pensar conceptualmente en lugar de mecánicamente. En este ejemplo, compartir pastel es un contexto intencional que refuerza la comprensión de los estudiantes de las fracciones como símbolos de partes de un todo. Adicionalmente, cuando los estudiantes utilizan estrategias y modelos que tengan sentido para ellos con el apoyo de sus profesores y compañeros, que se basan en el conocimiento actual a un ritmo adecuado.
aprendizaje de caracol
Muchos adultos asocian dibujos y manipulativos concretos con los alumnos pequeños. Imagine un aprendizaje kindergarten añadir usando dos cubos de conexión de color diferentes. Pero, el núcleo común hace hincapié en la importancia de introducir constantemente nuevos conceptos concreta y moverse hacia representaciones más abstractas en un ciclo de aprendizaje de caracol. Cuando los números se hacen más grandes o los problemas se hacen múltiples pasos, es normal que los estudiantes que “olvidan” estrategias avanzadas que han aprendido y se vuelven de nuevo a métodos concretos.
En el ejemplo de las empanadas de Ellis, el estudiante más concreta extrae del total, particiones, y cuenta para encontrar la diferencia. El estudiante más abstracta establece una ecuación y reconoce que resta repetida se puede calcular de manera más eficiente el uso de la multiplicación. En todos los enfoques, hay evidencia de la expresión 5 * ¾. Una respuesta de los estudiantes de destino durante el turno y hablar utilizará el lenguaje Historias de Matemáticas “En primer lugar me ... porque en la historia que dije…” para explicar el modelo. En este caso, durante el giro y las conversaciones que el maestro está monitoreando a los estudiantes la comprensión de que vemos el 5 * ¾ como el 5 porciones de tarta de ¾ para cada uno de los amigos. Cada representación mostró la 5 conjuntos de ¾ y luego llevando las cosas lejos de 9.
¿Cómo podemos impulsar a los estudiantes a pensar de forma abstracta y el uso de métodos eficientes sin imponer sobre su proceso de aprendizaje personal?
Las asociaciones significativas
Los estudiantes se acercarán naturalmente problemas de la historia utilizando diferentes estrategias y modelos, y esto crea oportunidades para el profesor para facilitar el aprendizaje centrado en el estudiante a través del habla pareja. la inserción de forma consistente un giro y charla antes de facilitar una discusión con toda clase de ayuda a los estudiantes a practicar la articulación de sus propias ideas y escuchar activamente a las ideas de un compañero antes de participar en el discurso de toda la clase.
Ya se trate de un grupo de dos o cuatro, que es más eficaz para los estudiantes del grupo en los grupos de habilidades mixtas de habilidades académicas, necesidades lingüísticas, la dinámica social, y el comportamiento.2 En el ejemplo de las empanadas de Ellis, estudiantes que se multiplicaron pueden compartir esta estrategia eficiente con un compañero que lleva a cabo la adición repetida. Un estudiante que utiliza un diagrama de cintas de concreto podría contar el resto de sectores para demostrar que sus pares cometió un error de cálculo en su ecuación. Es importante que los estudiantes están cuestionando constantemente entre sí, de manera que justificar su razonamiento se convierte innata, en lugar de un reflejo cuando un maestro señala un error. 2
Promover, que es esencial para los profesores y estudiantes para establecer normas asociadas que reflejan las habilidades de escucha activa y el respeto que se esperan de colegas profesionales:
- ¿Hay un orden asignado (Compañero A y B socio) o ¿Los estudiantes piden, “¿Quieres ir primero?”
- ¿Hay una señal que indica que el interruptor de socios?
- ¿Cómo se espera que los estudiantes para mostrar la escucha activa?
- ¿Qué idioma se pueden usar los estudiantes a estar en desacuerdo con respeto o hacer referencia de nuevo al problema historia?
Las normas deben ser fácilmente accesibles y revisados periódicamente para atender las necesidades de la cohorte.
A continuación se muestra un ejemplo de los socios de matemáticas-habilidades mixtas en el edificio de BVP en cada uno de los demás’ comprensión y vocabulario a través de un giro-and-Talk.
Mientras que el profesor recoge datos y busca trabajo de los estudiantes significativa para culminante, el giro y la charla ofrece a los estudiantes la oportunidad para flexionar muchas de las habilidades repetir en el Consejo Nacional de Profesores de Matemáticas (NCTM) Cinco estándares de procesos. la orientación del profesor se limita a establecer normas de conversación y la disponibilidad vocabulario matemático.
La investigación realizada por el NCTM establece que: “Los estudiantes que aprenden a articular y justificar sus propias ideas matemáticas, razón través de explicaciones matemáticas de sus propios y ajenos, y proporcionar una justificación de sus respuestas a desarrollar una comprensión profunda que es fundamental para su futuro éxito en matemáticas y campos relacionados “.1
recursos
1 Carpintero, et al. (2003). pensando Matemáticamente: La integración de aritmética y álgebra en las escuelas primarias.
2 Van de Walle, et al. (2008). las matemáticas de primaria y secundaria: la enseñanza de desarrollo.
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani


