Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana

Caza, no Pesca

¿Alguna vez ha lanzado una línea de pesca? La naturaleza de la pesca es que nunca se sabe exactamente lo que se obtiene. Director General de las Escuelas Poco frecuentes, Doug Lemov, recuerda a un líder en un taller que describe el poder de la elección de “caza sobre la pesca:”

La idea es que cuando se llame a los estudiantes y no tienen idea de lo que van a decir, esa es la pesca. Tú esperanza se obtiene una respuesta útil para la discusión o análisis, pero usted no sabe lo que se obtiene. No hay nada malo con la pesca-a veces es bueno ser sorprendido, pero a veces puede ser mejor para cazar-asignar la reflexión por escrito antes de la discusión y de circular durante la discusión de elegir estudiantes específicos para pedir a compartir ya que sus respuestas serán más productivos para discutir (a menudo porque desarrollaron una idea clave o cometió un error común a todos se puede aprender de). Se aporta un nuevo nivel de intencionalidad a las discusiones.¹

Como cazadores, los profesores pueden estampar puntos matemáticos claves de una manera oportuna, al mismo tiempo que facilita una discusión que se centra en torno a las ideas de los estudiantes y la voz del estudiante.

 

Todo está en el Protocolo

Dentro del protocolo de Historias de Matemáticas…

Después de resolver el problema historia usando un modelo representativo, los alumnos que abran y hablar con un compañero para compartir su modelo usando el lenguaje matemático y justifican su razonamiento. A medida que los estudiantes están compartiendo, el maestro utiliza una rastreador para registrar cómo los estudiantes individuales son la solución y medir rápidamente el porcentaje de la clase modela y resuelve correctamente.

Si la mayoría de los estudiantes son la solución correcta, este ser maestros 2-3 modelos en el tablero de menos a más sofisticada. El profesor pide a los socios a su vez-y-habla en respuesta a la siguiente pregunta: Lo que hace que estos modelos iguales o diferentes?

Esto a su vez-y-habla es fundamental para el maestro, que está a la caza de respuestas de los estudiantes que él o ella puede utilizar para elaborar una discusión significativa.

En la última semana de entrada en el blog, Hablé de los maestros utilizando un rastreador para recopilar datos en-el momento, que a su vez informa a la pregunta de discusión que piden a los estudiantes. ¿Cómo pueden los maestros escuchar en charla pareja y utilizar estratégicamente respuestas de los estudiantes a las embarcaciones de una discusión que se basa la comprensión del estudiante?

 

En contexto

Consideremos el siguiente problema historia:

Lally trae 2/3 de un galón de agua para la práctica de fútbol. Se suponía que debía llevar 1 1/2 galones de agua. La cantidad de agua adicional debe ha criado?

Los estudiantes deben darse cuenta de que no se puede sumar o restar distinto denominador. Pueden usar la multiplicación o partición para convertir a ⅔ 4/6 y 1 ½ a 9/6.

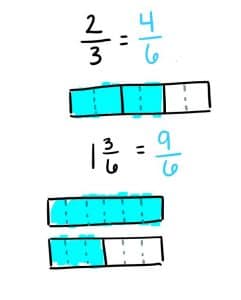
Los estudiantes pueden dibujar un vínculo número de interpretar el problema historia:

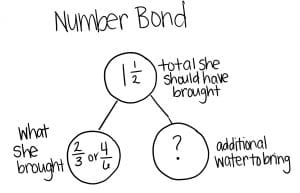
bonos números nos ayudan a ver la relación inversa entre la suma y la resta. Es compatible con los estudiantes, ya que interpretan la historia usando la información del problema.

Podemos contar la historia de dos maneras diferentes:

Adición: El agua ⅔ Lally ya efectuado, añade al agua extra es igual a 1 ½ . La respuesta es la cantidad añadida a ⅔ iguales 1 ½ .

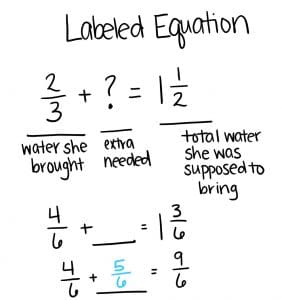
Sustracción: los 1 ½ Lally total de agua se supone que tiene, quitarle el agua ⅔ que ya trajo es igual a la cantidad más que debería haber traído. La respuesta es la diferencia 1 ½ – ⅔.

Al resolver este problema, hay varios puntos clave que los profesores pueden elegir para acabar con los estudiantes sobre la base de las tendencias que han notado en el trabajo académico cuando los estudiosos han trabajado en los tipos de problemas similares:

Punto clave 1

Necesitamos las mismas unidades para sumar o restar los números.

Punto clave 2

Podemos utilizar fracciones equivalentes para volver a escribir los números con unidades comunes.

Punto clave 3

La ecuación se escribe para modelar una situación podría ser diferente de la ecuación pensamos en resolver.

Punto clave 3 pide que los estudiantes sean pensadores flexibles. Hacer que los estudiantes comparten una variedad de modelos de ayuda a pensar profundamente acerca de las relaciones en matemáticas. Si un maestro observa más de la mitad de la clase de modelado correctamente, se elegirá 2-3 estudiantes con representaciones claras para compartir cómo se resuelven en la junta, entonces pregunta:

Estudiante 1 representado el exceso de agua con una ecuación de adición. Estudiante 2 representado el exceso de agua con una ecuación de la resta. ¿Cómo pueden ser correctas?

Los estudiantes participan en una vuelta y hablar con su pareja en respuesta a la pregunta de discusión. Señalan a los modelos en el tablero y utilizan el lenguaje del problema de palabras para justificar su razonamiento. A medida que los estudiantes están hablando, el maestro está escuchando a los estudiantes que pueden llamar en un orden que se basa en la comprensión de toda la clase.

Lo que se ve esto en el aula durante Historias de matemáticas?

 

Un ejemplo en Acción

Vamos a considerar los siguientes modelos de estudiante:

 

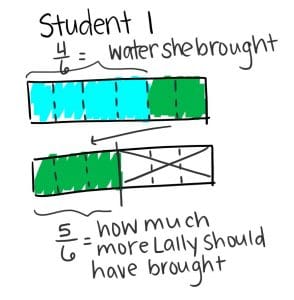
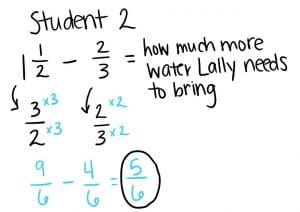
Una discusión con los estudiantes andamiaje predeterminados para invocan puede sonar algo como esto:

Profesor: __ ¿puedes empezar por compartir su interpretación del modelo de estudiante 1?

Respuesta 1: Estudiante 1 dibujó toda el agua, eso es 1 ½ , luego se dividieron el primero galón de agua en ⅔ y se repartieron para hacer la fracción equivalente 4/6. Ellos daban sombra al 4/6 y la calificó como “agua que ella trajo.” Entonces ellos contaron las sextas partes sombreadas, detenerse en un total de 1 ½ para obtener la cantidad más Lally debería haber llevado. Contaban ⅚. Lally debería haber llevado ⅚ galones más de agua.

Profesor: __ se puede compartir su interpretación del modelo del estudiante con la clase 2?

Respuesta 2: Estudiante 2 sabía que Lally trajo ⅔ de la cantidad total de 1 ½ , lo que significa que la diferencia es cuánto más se necesita para llevar. Se multiplicaron para hacer fracciones con denominadores comunes y escribió una ecuación para restar los numeradores. 9 sextos menos 4 sextos es 5 sextos (⅚).

Profesor: Si se utilizan diferentes estrategias, ¿cómo pueden ser correctas? __ se puede compartir su respuesta a la pregunta de discusión?

Respuesta 3: Estudiante 1 contado los sextos después de 4/6 para encontrar cuánto más Lally necesario añadir hasta un total de 9/6. Estudiante 2 utilizado la inversa de esta relación, cual es 9/6 menos 4/6. Ya sea que lo representan como suma o resta, a encontrar la pieza faltante, o la ⅚ que debería haber llevado a Lally.

 

Después de la tercera estudiante responde a la pregunta de discusión, el profesor afirma que esto es correcto y pedir a los demás a reformular el punto clave en sus propias palabras o demostrar que el punto clave es verdad utilizando un enlace serie. Un verdadero marcador de excelencia sería usando el rastreador de datos para llamar intencionadamente a los estudiantes que modelan de forma incorrecta. Están ahora interpretando correctamente el problema? Los estudiantes entonces registrar toda el punto clave en su papel.

 

Escuchando en una vuelta y hablar conversaciones (caza), maestros puedan asegurar la discusión de toda la clase está dirigido y alineados con el punto clave. Tenía el maestro en el ejemplo pescado llamando en las manos levantadas, la discusión podría haber sido confundido, resultando en un menor número de instantes de AHA y es menos probable duradera comprensión.

 

Qué dice la investigación?

La estructura y la pedagogía detrás del protocolo de 20 minutos Historias de Matemáticas refleja la lenta adopción de los Estados Unidos de enfoques para la enseñanza de las matemáticas que han demostrado su eficacia en los países del Este de Asia como China y Japón.

A principios de los años 90, un estudio de las clases de matemáticas en 800 escuelas primarias en todo Beijing, China; Sendai, Japón; Taipei, tawan; y Minneapolis y Chicago en los Estados Unidos observaron varias tendencias en los salones chinos y japoneses que eran menos comunes en las escuelas estadounidenses:

• La presentación de un concepto matemático en una variedad de formas,
• El instructor realizar como coordinador en lugar de un juez,
• Proporcionar experiencias concretas antes de enseñar conceptos abstractos, y
• El uso de técnicas que facilitan la comprensión conceptual (Sotavento, 1998).²

El diseño de las plantas de matemáticas se ocupa de estas áreas que están siendo pasados ​​por alto a menudo en la enseñanza tradicional de la matemática básica en los EE.UU., y estas prácticas crean participar más activamente los alumnos.

Cuando los maestros usan las respuestas a su vez-y-habla para planificar una discusión andamiaje, están actuando como coordinador. Promover, que son capaces de construir sobre la comprensión de toda la clase haciendo que los estudiantes descomponer el problema e interpretar una variedad de modelos que aumentan en complejidad.

 

recursos

¹ Lemov, Doug. (2015) Caza Versus Pesca.

² Ventilador, Lianghuo et al. (2004) Cómo china con las matemáticas. Perspectivas de información privilegiada.

 

Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani