Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
¿Por qué el aprendizaje entre iguales?
¿Alguna vez has estado en un comité? ¿Y en un grupo de estudio? O en un equipo? Peer-to-peer de aprendizaje se utiliza regularmente en las aulas y espacios de trabajo.
Cuando fue CEO de Pixar, Steve Jobs transformó famoso las sede de la empresa. El campus fue construido sobre el presupuesto de una película, aunque está diseñado con un solo uno baño en el atrio. Por qué?
“Si un edificio no anima [colaboración], si no se pierden una gran cantidad de innovación y la magia que está provocado por casualidad. Lo que hemos diseñado el edificio para que la gente a salir de sus oficinas y se mezclan en el atrio central con la gente que de otra manera no podrían ver “.1
Si usted es un empleado de una franquicia creativa multimillonaria, o un estudiante de 5to grado de aprendizaje acerca de las fracciones, hay una amplitud de la investigación que apoya la idea de que las ideas de comunicación y de intercambio con sus pares conduce a un aprendizaje más profundo.
En el último entrada en el blog, Hablé sobre el poder detrás de las historias planes de estudios de Matemáticas, que es una secuencia de problemas del mundo real que se basa en el rigor intencionadamente. Según lo definido por el núcleo común, rigor es un trípode bien equilibrada en la que los estudiantes persiguen:
- comprensión conceptual,
- habilidad y fluidez procedimental, y
- aplicación de las habilidades de resolución de problemas.
¿Cómo funciona el protocolo de Historias de Matemáticas reforzar peer-to-peer de aprendizaje? ¿Cómo pueden los maestros facilitan el aprendizaje entre pares eficaz y cuáles son los beneficios duraderos?
El Protocolo de Historias de Matemáticas
Durante el 20 minutos protocolo Historias Math, estudiantes de inmersión profunda en un problema de palabras conectado a un concepto matemático clave. Dentro del protocolo de Historias de matemáticas ...
Dentro de esta secuencia, estudiantes modelan y resuelven un problema historia de forma independiente antes de participar en una vuelta y hablar con un compañero para explicar su razonamiento. Este proceso difiere de aprendizaje colaborativo, en donde una asociación o grupo de estudiantes resuelven un problema juntos. Por volver a contar la historia de un problema y el uso de un modelo para justificar cómo resolvieron, los estudiantes están participando en peer-to-peer de aprendizaje.
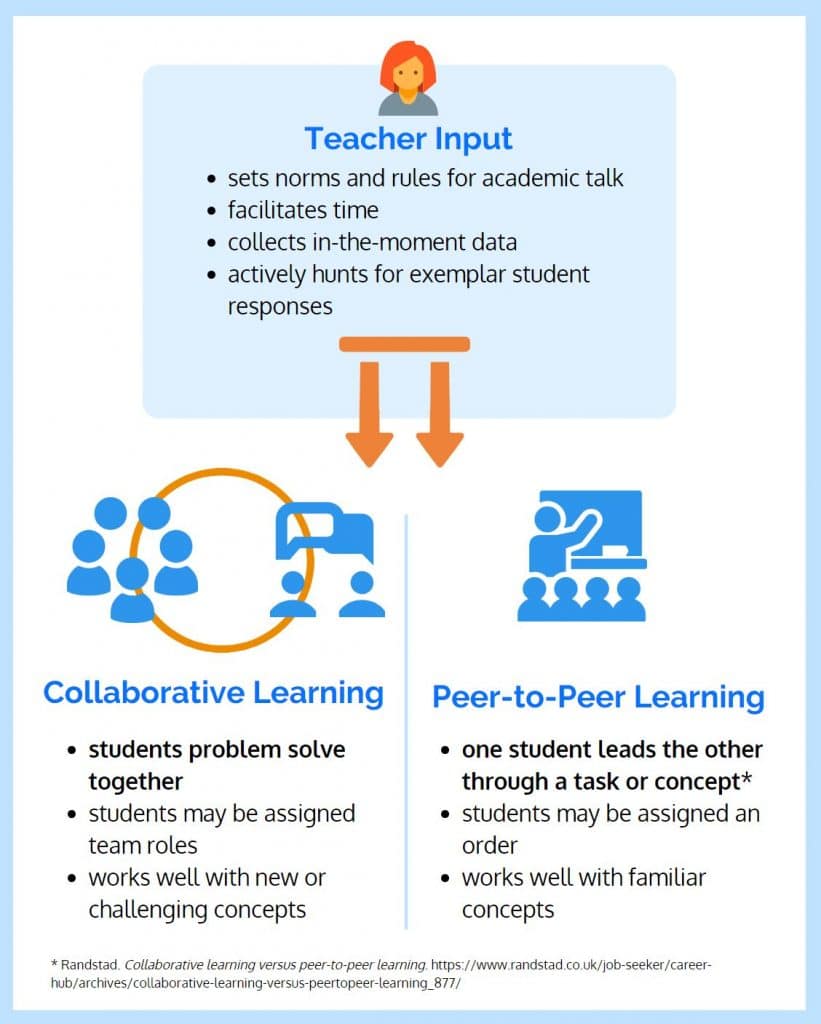
Peer-to-Peer Learning en Acción
Consideremos el siguiente problema historia:
María y su 5 amigos quieren dividir 3 brownies de manera uniforme. ¿Qué fracción de un brownie debe conseguir cada amigo?
Estudiante 1 y Estudiantes 2 resolver de forma independiente utilizando diferentes modelos para representar su pensamiento…
Estudiante 1
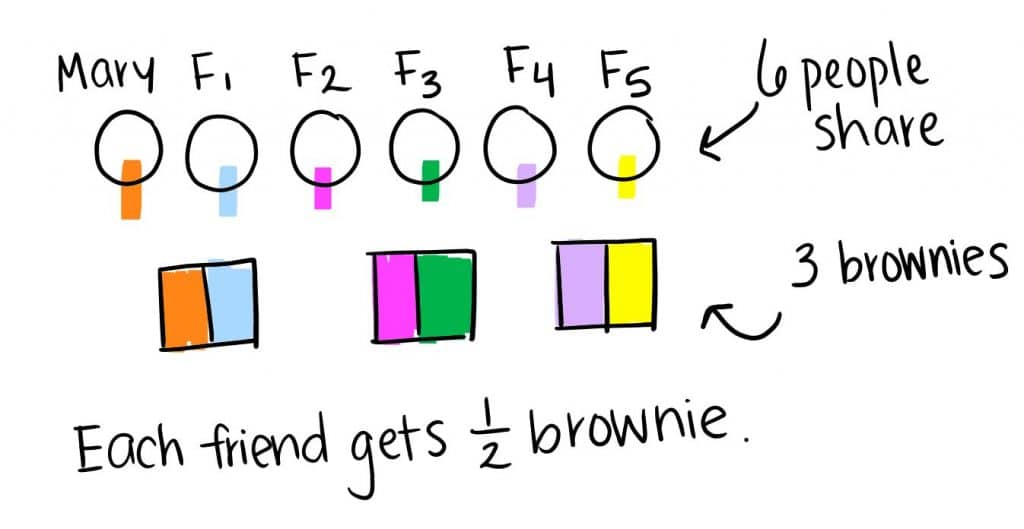Estrategia: Estudiante señala a la 6 personas que comparten (María y su 5 amigos). Al dividir cada brownie en media, el estudiante crea 6 piezas iguales. Cada una de las 6 amigos consiguen la mitad de un brownie.
Estudiante 2
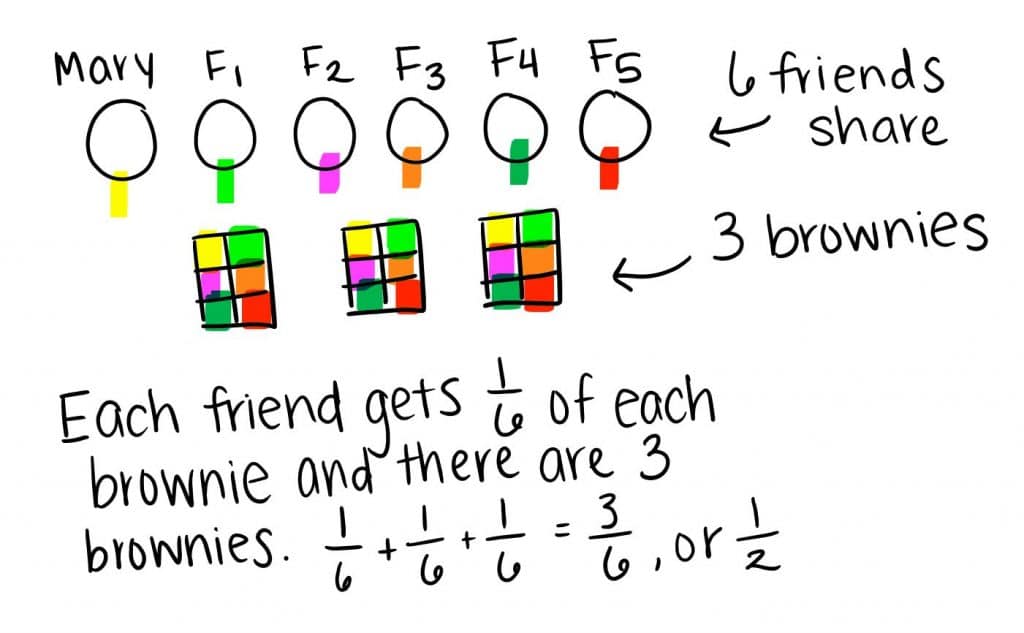
Estrategia: Estudiante señala a la 6 gente. particiones de estudiantes cada brownie en 6 a partes iguales, o sextos. Estudiante repite este proceso para cada brownie y añade los sextos, lo que resulta en cada amigo conseguir 3 sextos, 3/6 o ½ de un brownie.
¿Cuál es el beneficio de Estudiante 1 y Estudiantes 2 la comparación de las estrategias?
Estudiante 1 puede tener sentido número usado para visualizar intuitivamente que el corte de la 3 bizcochos de chocolate en medio generarían el doble de piezas para compartir–el mismo número que María y sus amigos. Este tipo de razonamiento es de gran alcance y cómo queremos que los estudiantes pueden visualizar y dar sentido a la historia de los problemas.
estrategia de dividir cada brownie por el número de individuos y repitiendo este proceso estudiante de 2 a replicar el número de brownies en el problema de palabras, 3, es más desordenado que el estudiante 1, pero es un método que sea transferible a los números más complejos. En otras palabras, podemos utilizar esta estrategia no importa la cantidad de brownies o el número de personas que están compartiendo.
Al participar en un giro y charla, Estudiante 1 y Estudiantes 2 cada uno aprender un nuevo enfoque para resolver el mismo problema, así como la práctica de la comunicación de su razonamiento a un compañero utilizando el lenguaje matemático. He aquí cómo Estudiante 1 y Estudiantes 2 puede explicar sus respectivos enfoques:
Estudiante 1: primero, Dibujé María y su 5 amigos, porque esas son las personas en el problema de palabras. Siguiente, Dibujé el 3 brownie porque dice que se separaron 3 brownies de igual. Al mirar a mi dibujo, Me di cuenta de que si el 6 la gente se dividieron en pares, Habían cada acción 1 duende. Asi que, Me dividir cada brownie por la mitad. Cada amigo debe recibir ½ brownie.
Estudiante 2: primero, Dibujé María y su 5 amigos, porque esas son las personas en el problema de palabras. Existen 6 gente. Entonces dibujé los tres bizcochos de chocolate. Empecé con el primer brownie y dividirlo en 6 piezas iguales, o sextos. Cada persona tiene ⅙ brownie. Todavía tenía 2 brownies de la izquierda, así que dividir la segunda brownie en sextos y luego la tercera brownie en sextos. ⅙ + ⅙ + ⅙ = 3/6, que es equivalente a ½ .
La mayoría de suma importancia, es que mediante la enseñanza de unos a otros cómo se aproximaban al problema, Estudiante 1 y Estudiantes 2 se ven obligados a cuestionar Si y cómo ambos son correctos.
Una discusión que profundiza la comprensión
A medida que los estudiantes están volviendo a contar el problema historia y justificar su razonamiento con una pareja, El profesor es la caza de trabajo del estudiante que él o ella puede poner de relieve para la discusión. Si el maestro ve que casi toda la clase resuelto correctamente, pueden optar por Estudiante 1 y Estudiantes 2 para explicar sus respectivos enfoques para la clase y pedir:
¿Cómo son estos enfoques diferentes?
Los estudiantes participan en un segundo giro y charla. La pregunta de discusión obliga a los estudiantes a volver a leer el problema y la razón historia desde la perspectiva de su pares con el apoyo de un proporcionado visual. Hay un aumento de buy-in, porque el modelo está discutiendo vino de un estudiante, en lugar del maestro.
En términos de los brownies de María, el concepto clave el maestro está llevando a los estudiantes a descubrir mediante la comparación de los diferentes enfoques es:
Estudiante 1 dividir cada brownie en media, y Estudiantes 2 compartida entre los cada brownie 6 amigos. Estudiante 1 dice que cada amigo recibe ½ brownie. Estudiante 2 dice que cada amigo recibe ⅙ de cada brownie, y aquí están 3 Brownies, por lo que cada amigo recibe 3 sextos. ⅙ + ⅙ + ⅙ es 3/6, o ½. Ellos tienen la misma respuesta, aunque Estudiante 1 dividido y Estudiante 2 adición repetida usado.
se muestra visualmente:
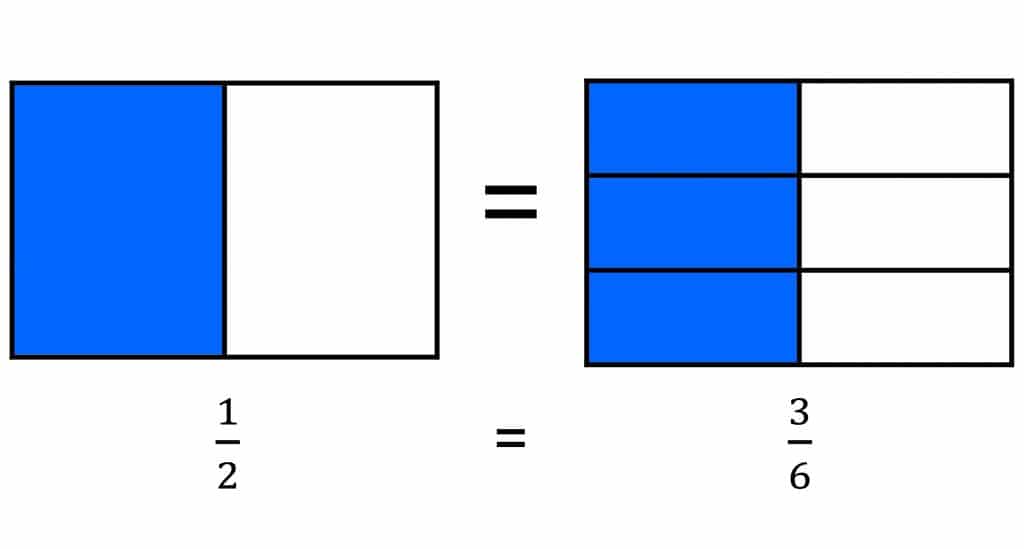
Mediante un razonamiento si y cómo ambas representaciones estudiantiles puede ser correcto, eruditos están haciendo sentido de fracciones equivalentes en el contexto del intercambio.
Es importante señalar que la mayor parte del aprendizaje ocurre cuando los estudiantes están emparejados intencionadamente en grupos de distintas capacidades de las habilidades académicas, necesidades lingüísticas, la dinámica social, y el comportamiento (Van de Walle, et al. 2008). Los estudiantes con diferentes puntos fuertes son más hábiles para ayudarse mutuamente. Por ejemplo, un idioma Inglés alumno se beneficia de ser emparejado con un estudiante que está utilizando el lenguaje matemático con precisión.
Peer-to-Peer Learning en las Normas
El aprendizaje entre iguales es un punto de acceso para las habilidades vitales dentro de los estándares de proceso NCTM y los estándares de la práctica matemática de la CCSS.2 los razonamiento y pruebas norma requiere que los estudiantes a criticar el razonamiento de los demás, y el comunicación norma pide a los estudiantes para justificar su razonamiento para construir un argumento viable.
brownie problema de María es una problema de reparto equitativo. El Instituto de Ciencias de la Educación (IES) recomienda el uso de actividades de reparto equitativo para desarrollar la comprensión conceptual de las fracciones.
Según los investigadores: “Los Estándares Estatales Comunes llaman para dividir círculos y rectángulos en partes iguales en primer y segundo grado. Por lo tanto, tendría sentido que los problemas de reparto por igual son una parte de la enseñanza en los niveles primarios de grado. sin embargo, es igual de importante la utilización de reparto equitativo de los problemas con los estudiantes mayores de perfeccionar y profundizar su comprensión de las fracciones (Empson & Levi, 2011).”3
Con demasiada frecuencia, los estudiantes confunden fracciones como algo separado de números enteros, en lugar de cantidades en una recta numérica al tanto de las mismas operaciones matemáticas. problemas de reparto equitativo de construir la comprensión conceptual mediante el uso de un contexto relacionables.
Qué dice la investigación?
Los investigadores apuntan a peer-to-peer aprendizaje en las matemáticas como beneficiosas para una multitud de razones.
Los estudiantes…
- habilidades de comunicación práctica y lenguaje preciso,
- experiencia de reducción de la ansiedad aula,
- ver su profesor se preocupa por su proceso de pensamiento, y
- ejercer mayor perseverancia en relación con los problemas difíciles.
Cuando los estudiantes aprenden a la espera de enseñar a otros, que de hecho puede alterar el proceso de aprendizaje “Promover un mayor esfuerzo para seleccionar los elementos relevantes y organizarlas en una representación significativa” (Benware y Deci, 1984).4 Cuando los estudiantes están enseñando el uno al otro, manda un mayor nivel de comprensión.
Investigador John Hattie ha pasado dos décadas estudiando el efecto de una multitud de características de educación– factores como la instrucción fónica, credibilidad maestro, y el tamaño de la escuela. En la más reciente clasificación, Patty ha combinado más de mil meta-estudios relativos a un cuarto de mil millones de estudiantes para determinar lo que más importa para el éxito del estudiante. Es evidente a partir de este fragmento de su análisis (Ve la tabla) que las estrategias como el aprendizaje en grupo colaborativo y la tutoría entre iguales generan una gran cantidad de progreso del estudiante a un bajo costo.5 Por ejemplo, el tamaño del efecto de tutoría entre iguales es dos veces el de la reducción de tamaño de la clase a menos de 20 estudiantes, una intervención que es cinco veces más caro para las escuelas.
Promover, cuando los maestros facilitan la enseñanza de los estudiantes entre sí, tienen más flexibilidad para recoger datos en-el momento y escuchar la vuelta y conversaciones. Esto conduce a la más frecuente y precisa respuesta de los estudiantes, que identifica de investigación de Hattie tiene un efecto enorme en el éxito académico de un estudiante.
recursos
1 Sede de Pixar y el legado de Steve Jobs.
2 NCTM. Los estándares del estado básico común para Matemáticas.
3 La introducción de fracciones a través del contexto, con énfasis en las progresiones Common Core. (2014)
4 Laal y Ghodsi. Beneficios de aprendizaje colaborativo. (2011)
5 El economista. La enseñanza de los maestros. (2016)
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani
