Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
¿Por qué los problemas de la historia?
Evan utiliza ⅔ taza de piña para cada batido hace. ¿Cuántas tazas de piña las utiliza para hacer Evan 6 batidos?
A viajes caracol ½ pulgada cada minuto. ¿Cuántos minutos se tarda en el caracol de viajar 5 pulgadas?
Edna está haciendo la mezcla del rastro. Y añade ⅝ tazas de cacahuetes, 2/8 tazas de pasas y almendras ½ taza. ¿Cuántas tazas de mezcla de frutos secos se hacen en toda ella?
Todas las preguntas anteriores son ejemplos de problemas de la historia fracción. Unidades sobre fracciones de enseñanza están llenas de porciones de alimentos, parcelas de jardín, y yardas de cinta. Por qué?
En mi último entrada en el blog, Hablé sobre el impacto en el aprendizaje del estudiante cuando los maestros caza intencional de respuestas de los estudiantes durante un giro-and-Talk para facilitar una discusión significativa, en lugar de pedir a los estudiantes al azar y esperar lo mejor. Esta semana damos un paso atrás para examinar el poder detrás de los estudiantes actuales problemas de la historia resolviendo durante Historias de matemáticas.
¿Cómo funciona la solución de problemas de la historia apoyan a los estudiantes en el desarrollo de habilidades conceptuales y procedimentales? ¿Qué deben educadores sudar cuando se trata de problemas de la historia de enseñanza?
Un alcance y secuencia que se basa en el rigor
Durante Historias de matemáticas, profesores facilitan una 20-protocolo minutos en el que los estudiantes inmersión profunda en un problema de palabras conectado a un concepto matemático clave. Dentro del protocolo de Historias de matemáticas ...

Las historias alcance y la secuencia Math se compone de 70 problemas de la historia, varios conjuntos que incluyen 10-13 problemas al mes. Esto permite a los maestros la flexibilidad para responder a los datos de la clase y repetir los tipos de problemas en la que los estudiantes necesitan pasar más tiempo. Para los problemas de la historia fracción quinto grado, Al principio del año escolar se centra en los tipos de problemas a partir del grado anterior.1 Nos Reloop problemas de la historia de la fracción de la calificación anterior, por lo que los estudiosos no pierden su aprendizaje fracción. En quinto grado, muchos programas de estudio (Participar como NY) no enseñan fracciones hasta que la tercera unidad. Al centrarse en los problemas de la historia fracción cuarto grado al comienzo del año, nos aseguramos de que los estudiosos están dispuestos a participar con rigurosa, grado de nivel de problemas de la historia tan pronto como sea posible.
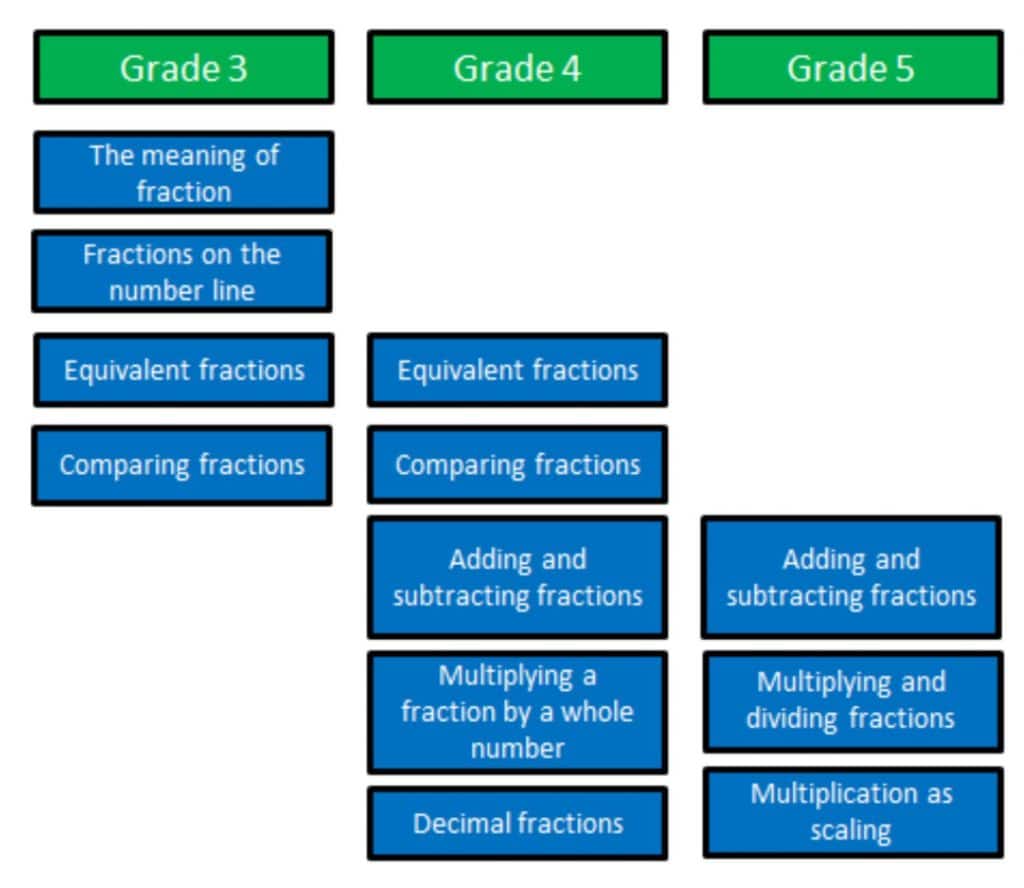
El problema Creación de juegos intencionadamente en el rigor. Por ejemplo, los estudiantes a resolver problemas con unidades comunes para 1-2 meses antes de distinto denominador se introducen. Inicialmente, distinto denominador se restringen a mitades, cuartas, y octavos y los estudiantes sólo están transformando una fracción. Este andamiaje permite a los estudiantes practicar la partición con las unidades familiares y tienen sentido de la equivalencia de modelos visuales en lugar de algoritmos.
Los estudiantes están expuestos a mitades, cuartas, y octavos a partir de 3er grado, y estas unidades familiares son más fáciles de crear particiones. Adicionalmente, utilizando un modelo de reescribir una fracción es un enfoque basado en la evidencia que permite a los estudiantes desarrollar una comprensión real de lo que es una fracción equivalente y su utilidad en la adición o sustracción diferencia de las unidades.2
La naturaleza de los conjuntos de problemas andamiaje es que los estudiantes están utilizando modelos para aplicar nuevos conceptos antes de que se les enseña explícitamente en lecciones básicas. Esto crea una poderosa dinámica del aula en la que el profesor es un facilitador más que profesor y los estudiantes tienen la agencia. Investigador John Van De Walle sugiere que:
Un error común es que el maestro comprensión conceptual de suma y resta de fracciones debe preceder a su trabajo con la aplicación. Más bien, comprensión conceptual y la aplicación de trabajo juntos como estudiantes aprovechan el razonamiento de la vida real a cuestionar si y por qué sus representaciones y respuestas tienen sentido.
Muchos profesores creen que los estudiosos no pueden aprender algo hasta que se enseña explícitamente. Creemos que con las estructuras y soportes adecuados durante Historias de matemáticas, los estudiantes pueden desarrollar modelos y soluciones creativas a problemas difíciles sin instrucción explícita. Promover, cuando los estudiosos son los agentes de su propio aprendizaje basado en el descubrimiento, es más probable que lo que han aprendido es “pegajosa”. En otras palabras,, que se acuerden de cómo y por qué se acercaban a los tipos de problemas como lo hicieron y aplicar este conocimiento avanzar.
Como el núcleo común Define Rigor
A través de la comparación y análisis de los resultados de TIMSS internacionales, Básico común ha identificado tres turnos en las matemáticas para aumentar la universidad y la carrera de preparación para los estudiantes de América:
- Atención: Concentrarse fuertemente en las normas se centran
- Coherencia: Piense través de los grados y enlace a los principales temas en grados
- Rigor: En los temas principales, perseguir la comprensión conceptual, habilidad y fluidez procedimental, y la aplicación
Rigor según lo definido por el núcleo común no significa más duro. Rigor en matemáticas es un trípode bien equilibrado en el que cada área requiere la misma intensidad en el tiempo, ocupaciones, y recursos3 :
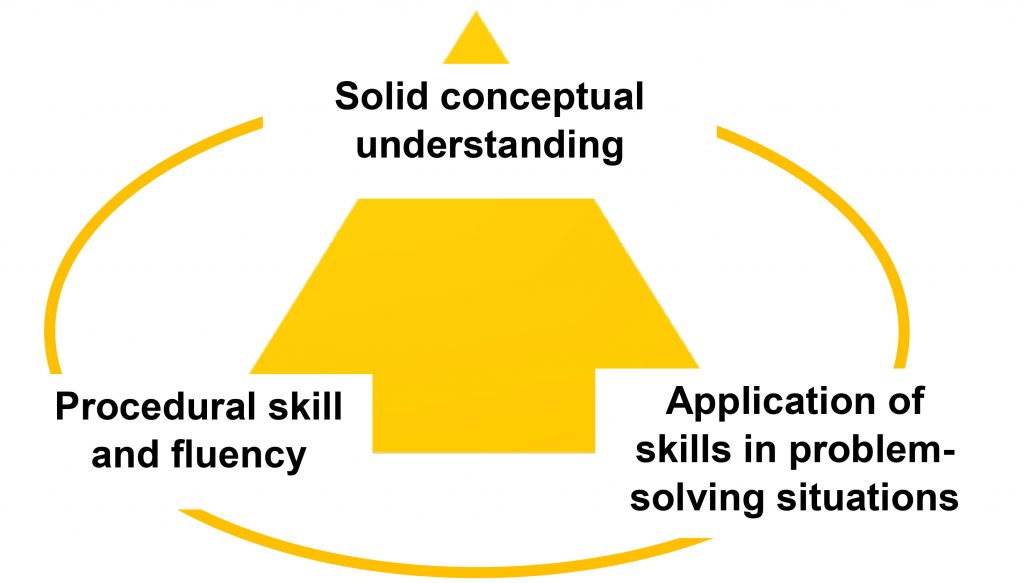
Cuando los estudiantes son la solución de problemas de la historia en Historias de matemáticas, que están flexionando los músculos cognitivos en cada una de estas áreas. Los estudiantes están haciendo significado de las habilidades matemáticas mediante su aplicación a situaciones del mundo real, tales como la búsqueda de denominadores comunes que agregar los ingredientes en una receta. problemas de la historia permiten la comprensión conceptual más profundo, permitiendo el acceso a los estudiantes a una variedad de enfoques en lugar de un procedimiento rutinario debido a que el profesor elige ejemplos de trabajos de alumnos para discutir como parte del protocolo. Finalmente, las normas proporcionan puntos de referencia de fluidez apropiadas para el grado. Los alumnos practican funciones básicas (e.g. añadir / restar dentro 1,000,000 y la multiplicación de varios dígitos) durante un tiempo de instrucción diferente o como tarea. velocidad y la precisión de un estudiante se convierte en un activo para la manipulación y la comprensión de los conceptos más complejos cuando están resolviendo un problema de matemáticas historia durante Historias.
Cara o cruz? Una forma de complementar los problemas de la historia
Sabemos que la historia de los problemas importantes. Asi que, ¿qué pueden hacer los educadores cuando se encuentran con los estudiantes que son problemas descremada Historia de la lectura en lugar de pensar críticamente?
Si bien creemos en el uso del protocolo de Historias de matemáticas para aumentar la capacidad de los estudiosos de entender conceptualmente y resolver los problemas de la historia, también reconocemos que hay otros enfoques fuertes de resolución de problemas.
El Consejo Nacional de Profesores de Matemáticas (NCTM) y muchos entrenadores de matemáticas sugerir la utilización de sin cabeza y rabón problemas de la historia para animar a los estudiantes a pensar profundamente sobre el idioma, contexto, y la estructura de un solo problema.
Considere el siguiente problema historia a partir de las historias de matemáticas:
La familia de Tompkins posee una granja. Su propiedad es 2 1/2 millas de ancho y 4 1/2 millas de largo. ¿Cuál es el área total de sus tierras en millas cuadradas?
UN rabón problema de palabras es uno que falta una pregunta. Aquí está escrito como un problema de palabras sin cola:
La familia de Tompkins posee una granja. Su propiedad es 2 ½ milla de ancho y 4 ½ millas de largo.
Los estudiantes trabajan en asociaciones o grupos para grabar lo que saben y no saben y generar posibles preguntas. Posibles preguntas generados por los estudiantes:
- ¿Cuál es el área total de la finca?
- ¿Cuánto tiempo es la granja que ancho?
- Si la familia quiere Tompkins 16 millas cuadradas de tierras de cultivo, ¿cuáles son algunas nuevas dimensiones posibles?
UN sin cabeza problema historia es una que da tan poca información como sea posible. Este es el problema de palabras sin cabeza:
La familia de Tompkins posee una granja. ¿Cuál es el área total de sus tierras en millas cuadradas?
Posibles pautas de maestros:
- ¿Tenemos suficiente información para responder a la pregunta?
- ¿Qué información necesitamos?
- Si te dijera que la granja es Tompkins 2 ½ millas de ancho, esto sería suficiente información? Por qué o por qué no?
Los estudiantes trabajan en asociaciones o grupos para discutir la información que se da y qué información se necesita para resolver el problema. sin números, los estudiantes no pueden saltar a los números de taponamiento en una ecuación. Deben analizar el contexto, idioma, y la estructura del problema. Una ventaja de esto es que apoya a los estudiantes en el reconocimiento de patrones entre los tipos de problemas a través del tiempo.
problemas sin cabeza y sin cola historia emulan los cálculos de no intervención que vemos en el mundo real. coordinador de las matemáticas Tim McCaffrey se describen las tareas sin cabeza como cómo funciona realmente el mundo. “Empezamos con una pregunta que nos preguntamos acerca, y tenemos que salir a buscar información relevante “.
La investigación ha demostrado que la conexión de las matemáticas al mundo real aumenta la motivación y la comprensión de los estudiantes, así como los prepara para espacios de trabajo que requieren conocimientos matemáticos.
Muchos de nosotros crecimos en las aulas que se enorgullecían de cálculo y de hecho la fluidez rápida. ¿Alguna vez ha tenido una prueba de “Minuto Loco”? Aunque la fluidez sigue siendo importante, es sólo una pata del trípode. Ejercicios de buceo profundo en problemas del mundo real son la clave para recordar a los estudiantes que los matemáticos son pensadores críticos y solucionadores de problemas–no calculadoras.
recursos
1 ilustrativos Matemáticas.
2 Van de Walle, John et al. (2013) Las matemáticas de primaria y secundaria: Enseñanza Desarrollo.
3 Lograr el Núcleo. (2016) Introducción a los turnos de matemáticas.
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani


