By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern

Partner Up

Have you ever had a lab partner? A marital partner? What about a turn-and-talk partner?

Walk into Blackstone Valley Prep during Math Stories and you’ll see students leaning in and politely taking turns explaining their mathematical models and solutions. They nod, ask their partner questions, and sometimes express confusion. Purposeful partnerships support students as they explain representational models, articulate key concepts, and develop new strategies for finding solutions through meaningful discourse.

In last week’s blog post, I spoke about the importance of scholars visualizing a story problem in context before creating a model that makes sense to them. Once students have represented their thought process in a clearly labeled model and solved, how can teachers use intentional partnerships to build meaningful dialogue regarding mathematical concepts?

As part of the Math Stories protocol, students listen as the story problem is read 2-3 times and visualize what’s happening, represent using a model that supports their visualization, and turn-and-talk with a partner to explain their reasoning.

After 2-3 scholars present their approach to the class, partners engage in a second turn-and-talk to discuss a teacher-generated question addressing the lesson’s key point.

Why is this first turn-and-talk beneficial for students?

 

Concrete and Abstract Representations

Students approach story problems in different ways. It’s important for students to model in the way that makes most sense to them because this leads to powerful conversations, rather than a stagnant academic culture where students are coached to represent in the same way. How concrete or abstract a student’s process is depends on:

• how they visualized the story problem
• what strategies they’ve been taught, and
• how confident they feel executing certain skills.

Let’s consider the following story problem:

Ellis bakes 9 pies. He gives 3/4 of a pie to each of his 5 friends. How much pie does Ellis have left?

Visual:

Some students will imagine nine pies cut into fourths. They shade 3 fourths five times to represent the portions Ellis gives to his friends. They find the total leftover by counting the unshaded fourths.

Model: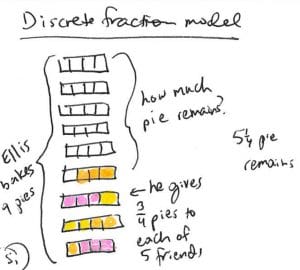

A discrete fraction model is used to show partitioning and iteration.

Knowledge:

They use their knowledge of fractions and part-part-whole relationships to count the unshaded fourths and make the connection that this is the difference, or what is left over.

---

Visual:

Some students will imagine a subtraction number sentence. They start with nine pies. They subtract ¾ five times for each friend Ellis gives pie to. The difference is how much pie Ellis has left over.

Model: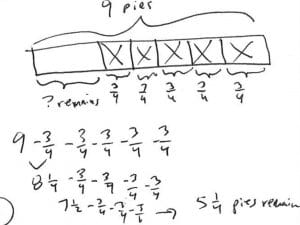

A generic tape diagram is used to show partitioning. An equation is used to show repeated subtraction.

Knowledge:

They use their knowledge of halves and fourths (benchmark fractions) to subtract five times.

---

Visual:

Some students will imagine a subtraction number sentence. They start with nine pies. They recognize that subtracting ¾ five times is the same as subtracting the product of ¾ * 5 from 9, or 3 ¾ .

Model: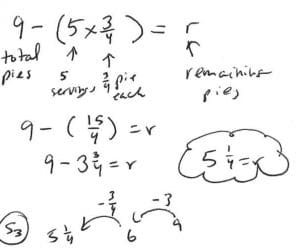

A labeled equation is used to show the total number of pies, 9, and the amount given away (5* ¾).

Knowledge:

They use their knowledge that repeated addition/subtraction is the same as multiplication to write the equation 9 – (¾*5) . Further, they know that when subtracting an improper fraction from a whole number, it’s cleaner to convert it into a mixed number, so you can subtract the whole and then the parts.

It’s critical that students are given story problems with varying operations, contexts, and complexity, so that they’re encouraged to think conceptually rather than mechanically. In this example, sharing pie is an intentional context that strengthens students’ understanding of fractions as symbols for parts of a whole. Additionally, when students use strategies and models that make sense to them with support from their teachers and peers, they build on their current knowledge at an appropriate pace.

 

Spiral Learning

Many adults associate concrete drawings and manipulatives with early learners. Imagine a kindergartener learning to add using two different color connecting cubes. But, the Common Core stresses the importance of constantly introducing new concepts concretely and moving towards more abstract representations in a cycle of spiral learning. When numbers get larger or problems become multiple steps, it’s normal for students to “forget” advanced strategies they’ve learned and turn back to concrete methods.

In the example of Ellis’ pies, the most concrete student draws the total, partitions, and counts to find the difference. The most abstract student sets up an equation and recognizes that repeated subtraction can be calculated more efficiently using multiplication. In all approaches, there is evidence of the expression 5*¾. A target student response during the turn and talk will use the Math Stories language “First I… because in the story it said…” to explain the model. In this case, during turn-and-talks the teacher is monitoring for students understanding that we see the 5*¾ as the 5 servings of ¾ pie for each of the friends. Each representation showed the 5 sets of ¾ and then took that away from 9.

How can we push students to think abstractly and use efficient methods without imposing on their personal learning process?

 

Meaningful Partnerships

Students will naturally approach story problems using different strategies and models, and this creates opportunities for the teacher to facilitate student-centered learning through partner talk. Consistently inserting a turn-and-talk before facilitating a whole class discussion helps students practice articulating their own ideas and actively listening to a peer’s ideas before participating in whole class discourse.

Whether it is a group of two or four, it’s most effective to group students in mixed-ability groups by academic skills, language needs, social dynamics, and behavior.² In the example of Ellis’ pies, students who multiplied can share this efficient strategy with a peer who performed repeated addition. A student who used a concrete tape diagram might count the remainder of pie to prove that their peer made a computational error in their equation. It’s important that students are consistently questioning each other, so that justifying their reasoning becomes innate, rather than a reflex when a teacher points out an error. ²

Further, it’s essential for teachers and students to set up partner norms that mirror the respect and active listening skills expected from professional colleagues:

• Is there an assigned order (Partner A and Partner B) or do students ask, “Do you want to go first?”
• Is there a signal indicating that the partners switch?
• How are students expected to show active listening?
• What language can students use to respectfully disagree or refer back to the story problem?

Norms should be readily accessible and revisited periodically to address the needs of the cohort.

Below is an example of mixed-ability math partners at BVP building on each others’ understanding and vocabulary through a turn-and-talk.

While the teacher collects data and looks for meaningful student work to highlight, the turn-and-talk gives students the opportunity to flex many of the skills iterated in the National Council of Teachers of Mathematics’ (NCTM) Five Process Standards. The teacher’s guidance is limited to setting conversation norms and providing mathematical vocabulary.

Research by NCTM states that: “Students who learn to articulate and justify their own mathematical ideas, reason through their own and others’ mathematical explanations, and provide a rationale for their answers develop a deep understanding that is critical to their future success in mathematics and related fields.”¹

Resources

¹ Carpenter, et al. (2003). Thinking Mathematically: Integrating Arithmetic and Algebra in Elementary Schools.

² Van de Walle, et al. (2008). Elementary and middle school mathematics: teaching developmentally.

 

Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani