By Steph Primiani, Director of STEM

Fractions in the Common Core

Many teachers aren’t teaching fractions correctly because many teachers weren’t taught how to understand fractions.

The teaching and learning of fractions is notoriously associated with memorizing procedures. It is this lack of sense making, so pervasive in traditional math instruction, that leads to frustration, surrender, and even failure.¹ The memorization of procedures is also how most adults were taught fractions as children. The Common Core Math fraction standards, however, call for students to use visual fraction models and equations to represent problems, explain why fractions are equivalent, and justify conclusions with fraction comparisons.

The question is: How can we support educators who were taught fractions procedurally to both understand and teach fractions conceptually?

 

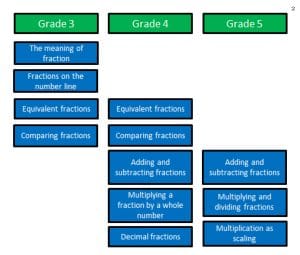
Tip 1: Use Contexts

John Van De Walle et al suggests that the most effective fractions instruction requires the teacher to “help students understand why procedures for computations with fractions make sense” (Siegler et al., 2010). They suggest effective fraction computation instruction must: (1) use contexts, and (2) use a variety of models.

In my first blog post, I mentioned that Blackstone Valley Prep is setting out to improve 5th grade fraction outcomes by engaging in a structured Math Stories protocol. Math Stories tackles the common teacher misconception that a conceptual understanding of adding and subtracting fractions must precede application. Rather, in Math Stories, conceptual understanding and application work together as students leverage real life reasoning to question if and why their representations and answers make sense.

No area of elementary mathematics is as mathematically rich, cognitively complicated, and difficult to teach as fractions. John P. Smith III (2002, p. 3)

Tip 2: Use a Variety of Models

Jessa drinks 2/5 liters of water in the morning and 1/2 liter of water in the afternoon. How much water did Jessa drink in the morning and afternoon combined?

Most adults were taught to solve this problem like this:

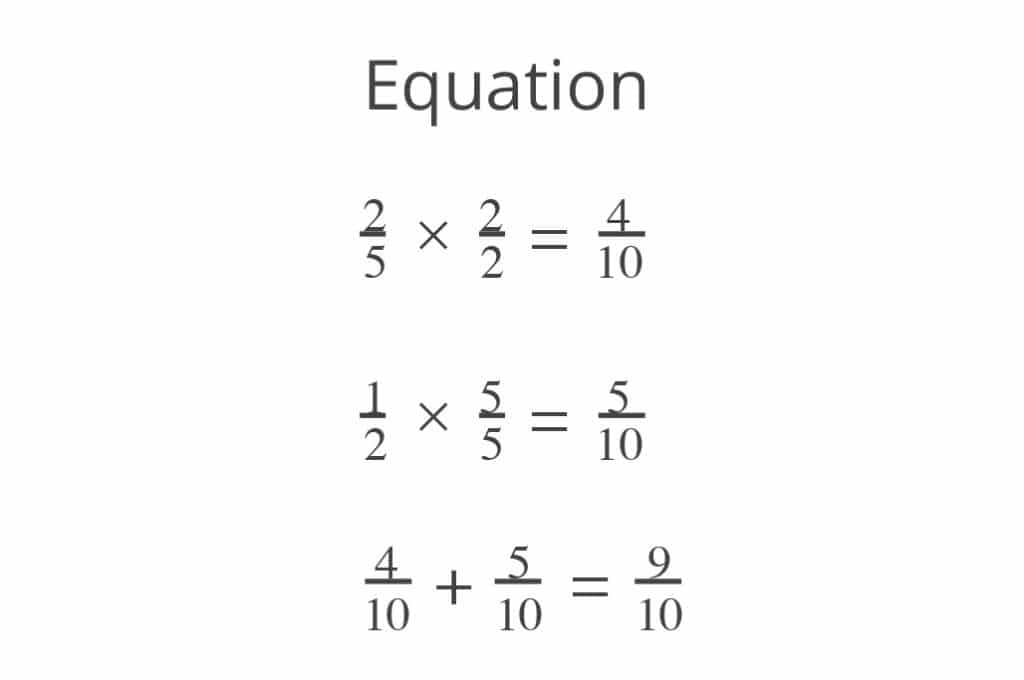
What if, instead, you had learned how to represent the problem like this:

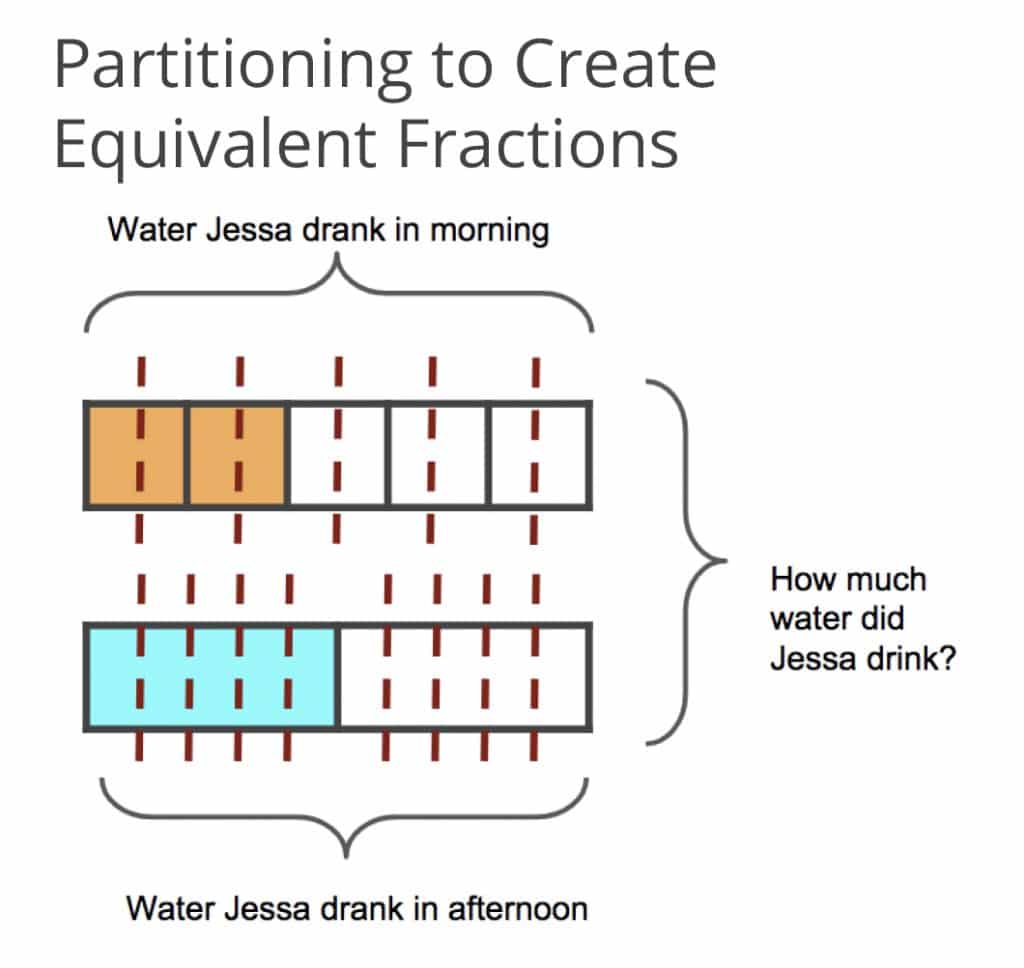
Or like this with a Tape Diagram (TD):

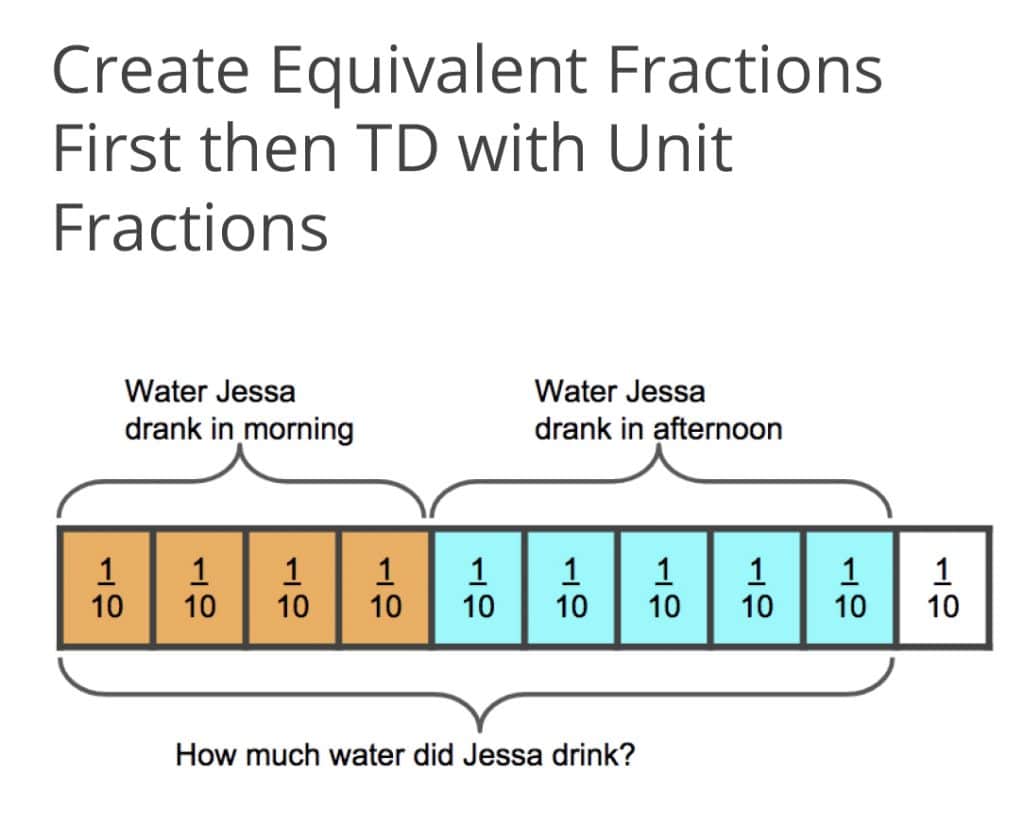
Or like this:

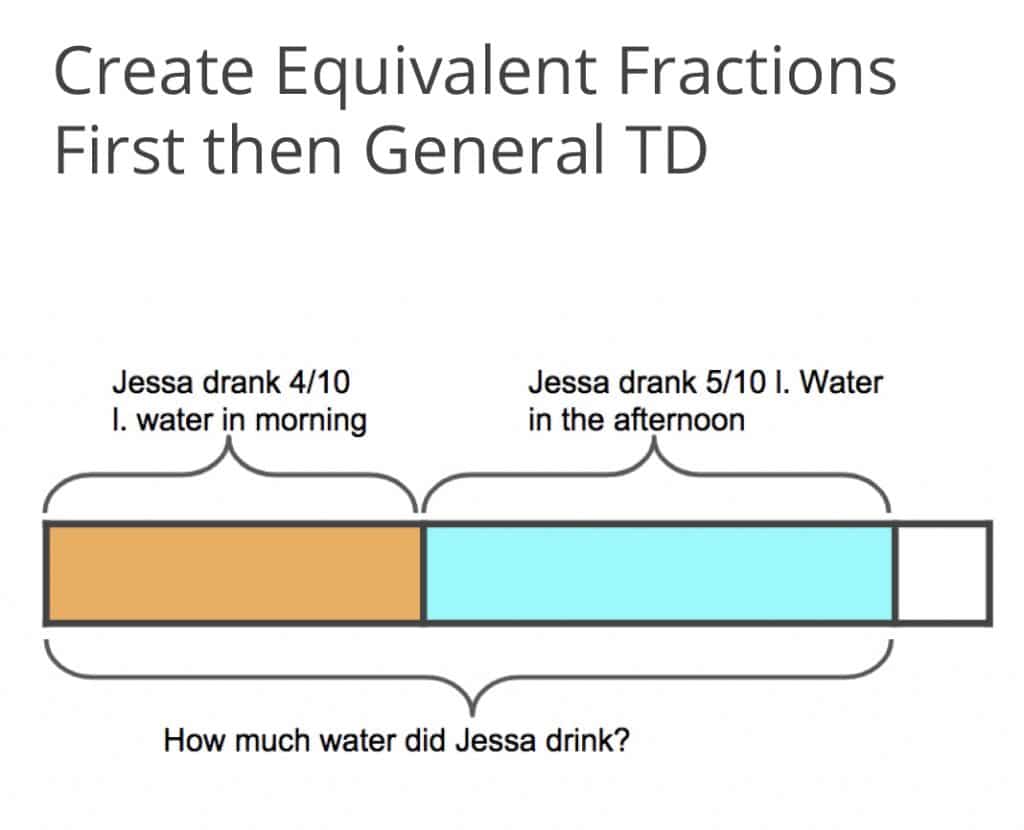
When 5th grade teachers at BVP prepare to teach a Math Stories lesson, they first must visually model the story in at least three different ways. This not only helps them think through the different student models they will encounter, but also helps to build deeper content understanding for the adults who are used to solving problems algebraically. If we don’t support our teachers in learning how to visually represent fraction stories, how can we expect our students to do well?

 

Want to Learn More?

In the next few posts, we will explore the different parts of the Math Stories protocol as well as how teachers plan for fraction story problem instruction.

Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani.

 

Resources

¹ The Challenge of Fractions, NCTM.

² Image taken from https:www.illustrativemathematics.org/progressions