By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
Don’t Leave it to Chance
How do you make important decisions? Do you flip a coin? Consult a confidante? What about using purposeful data collection?
Walk into Blackstone Valley Prep during Math Stories and you won’t see the teacher at the front of the room lecturing. Instead, Miss Palumbo gives instructions and students hurriedly begin sketching mathematical models that represent their thinking. A few minutes later, she sets a timer under the overhead projector and the buzz of academic dialogue fills the room as scholars turn to a partner to explain their model and justify their reasoning. She isn’t intervening or pointing out errors. She’s busy aggressively monitoring, looking at student work. Rather than focusing on compliance or using a checklist merely to mark if a student solved the problem correctly, teachers are using a data tracker to record the specific strategies and misconceptions they see in student work.
In last week’s blog post, I spoke about the importance of assigning intentional mixed-ability partnerships to expose students to new strategies and strengthen mathematical vocabulary. As students model and then turn-and-talk in partnerships, what data is the teacher collecting? How does in-the-moment data collection inform teaching and learning?
A Spectrum of Student Work
The Math Stories protocol includes an Intellectual Prep template. For each story problem, teachers prepare by finding the solution themselves. They record:
- the big idea/key points,
- a range of anticipated exemplar student models,
- possible misconceptions,
- discussion questions based on students’ understanding, and
- target responses.
This process helps teachers internalize key math objectives and strategies for the specific math story. When teachers are fluent in the math concepts, they can devote more energy to monitoring for understanding and making critical decisions.
Let’s consider the following story problem:
Janae drinks 7/8 of a quart of water. Javon drinks 1/2 a quart of water. How much more water did Janae drink than Javon?
Visual:
Some students will imagine two quart-sized water jugs. Janae’s jug is divided into 8 equal parts, and she drinks 7 eighths. Javon’s jug is divided into 2 equal parts, and he drinks 1 half. The solution can be imagined as the extra water Janae drinks as compared to Javon.
Model:
A discrete fraction model is used to show partitioning. The tape diagrams are lined up evenly in order to compare two quantities and find an equivalent fraction.
Knowledge:
Students use their knowledge that how much more is asking us to compare the amounts of water Janae and Javon consumed. In other words, find the difference. But, we cannot add or subtract numbers unless we have the same units. Students know we can find equivalent fractions of 1/2 by partitioning a tape diagram. By cutting 1/2 into fourths and then again into eighths, it’s evident that 1/2 is equal to 4 eighths (4/8). Students line up the tape diagrams and find the difference by counting the “extra” amount of water that Janae drank.
Visual:
Some students will imagine a subtraction number sentence. How much more means that the problem is asking for the difference between two quantities, in this case the extra amount of water Janae drinks as compared to Javon. 7/8 – 1/2= ___.
Model:
Students represent the information from the story problem using a labeled equation with the equivalent fraction.
Knowledge:
Students use the knowledge that to subtract fractions, we must have equivalent units. Students reason that 1/2 is a familiar unit fraction that can be transformed more easily than 7/8. 8 is equal to 2 groups of 4, so one half of 8 can be written as 4/8. Now we are subtracting 4 eighths from 7 eighths, which is 3 eighths (3/8).
Misconceptions
In terms of the Janae and Javon story problem, there are several possible errors students may make:
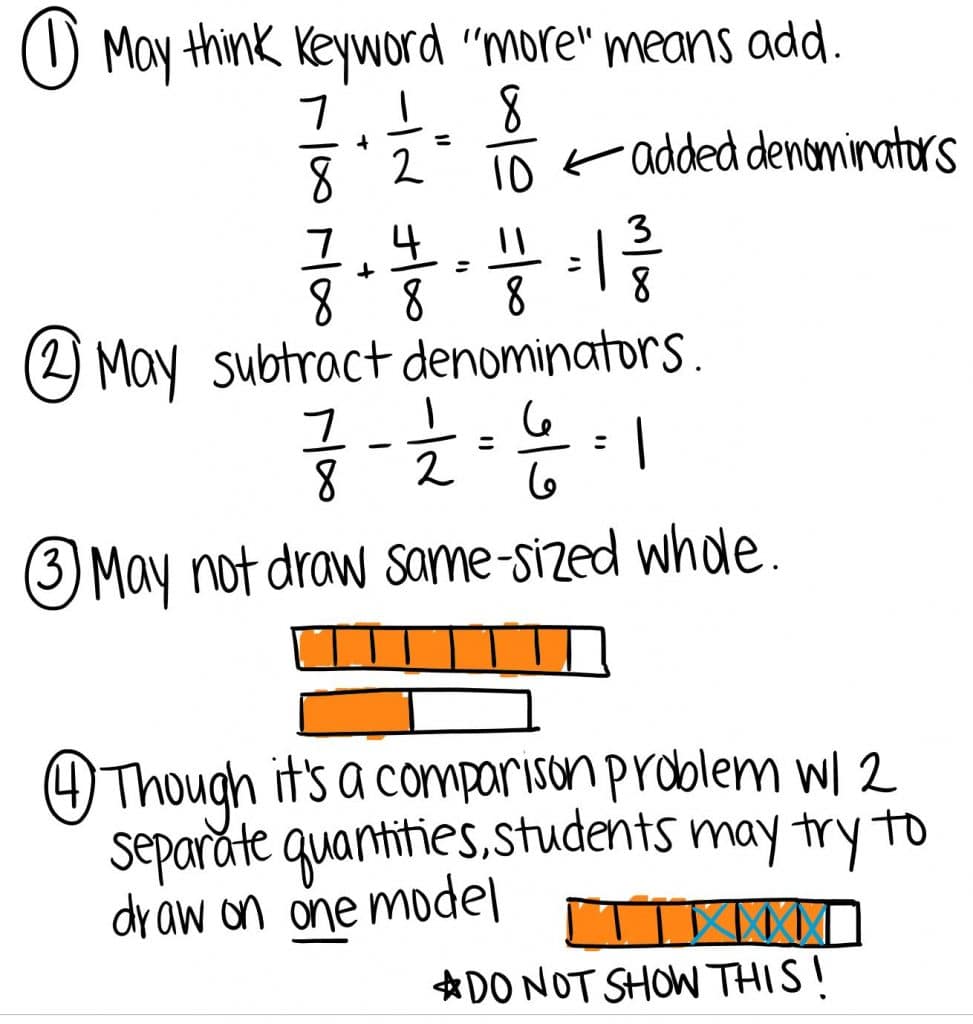
Misconceptions are developmentally appropriate and part of the learning process. They’re not errors as much as they’re valuable signals that a mathematical concept needs to be revisited. Further, misconceptions allow the teacher to facilitate a discussion in which students practice justifying their reasoning and using relevant vocabulary.
Watching vs. Aggressive Monitoring
Managing Director of the Uncommon Schools, Taxonomy Project and author of Teach Like a Champion, Doug Lemov, describes a key difference between teachers watching vs. aggressively monitoring students. Here is an excerpt from Teach Like a Champion, Field Guide 2.0:
The legendary basketball coach John Wooden offered this advice to teachers…: “Never mistake activity for achievement.” A busy gym with sneakers squeaking or a classroom full of pencils scratching is evidence of activity. This is often a good thing, but different from and easier to spot than achievement—a gym or a classroom that yields students who pass and move or factor equations impeccably.
Aggressive monitoring is focused on learning rather than management, and Lemov suggests teachers track two key indicators: specific errors and success points. As part of the protocol, teachers predetermine what quality student work should look like, as well as anticipating pitfalls, and the purpose of aggressive monitoring is for teachers to observe patterns in student work to know how to adjust their teaching in response. Additionally, research with Uncommon Schools suggests that aggressive monitoring messages to students that their effort is valued and the quality of their work matters.2
Using a Data Tracker
As mentioned above, a key tenet of math stories is monitoring aggressively while students model and retell the story problem and explain their representational model to a partner. Using a data tracker, the teacher records how individual students are solving and can quickly gauge what percent of the class modeled and solved correctly. There are three ways to respond to student data depending on the quality of student work:
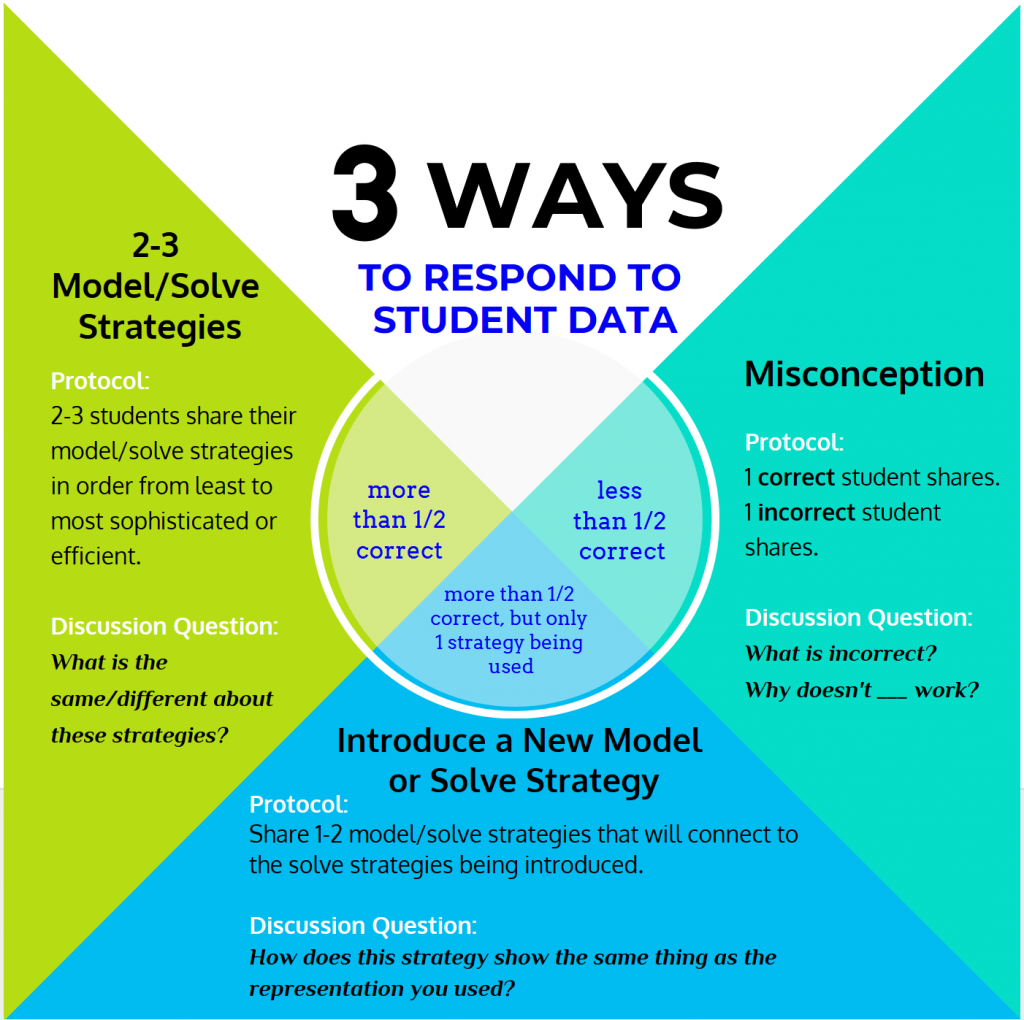
What does this look like in a classroom during Math Stories?
Example 1
Data Tracker:
![]()
We can see from the teacher’s data tracker that a little more than half the class solved correctly. Three students used a discrete fraction model correctly and two used a labeled equation correctly.
Protocol: The teacher chooses at least two students to share, one with a discrete fraction model and one with a labeled equation. By discussing how these two strategies are represent the same idea, students are exposed to different approaches and pushed to compare them for efficiency.
Discussion Question: What is the same/different about these strategies?
Example 2
Data Tracker:
![]()
We can see from the data tracker that a third of the class solved correctly, and a majority of students shared the misconception that the language “how much more” in the story problem is asking us to add.
Protocol: The teacher chooses a student who incorrectly added and a student who modeled finding the difference to facilitate a discussion around debunking the misconception. By having to justify their reasoning using the context of Janae and Javon, students better understand “how much more” and the conceptual differences between operations.
Discussion Question: Which model accurately represents the story?
Example 3
Data Tracker:
![]()
We can see from the data tracker that the majority of the class solved correctly, but students only used a discrete fraction model to solve.
Protocol: In this case, the teacher will use a student’s model to guide students to write the corresponding labeled equation.
The teacher may introduce the model by saying: “I saw a student last year…” or “A student in another class…” to maintain student-led learning even when key concepts are absent from the student work that day.
Discussion Question: How does this strategy show the same thing as the representation you used?
Why It Matters
Research around language and mathematics indicates that when students are taught communication skills, reasoning together in a group discussion improves individual learning and understanding of mathematical concepts.1 By quickly assessing student work and listening to turn-and-talk conversations, teachers can choose discussion questions that make the most impact on students’ understanding.
In each data tracker example, the teacher uses actual student work to respond to class patterns, rather than relying on a hunch. This approach ensures that each lesson is active–dissolving misconceptions, comparing an array of strategies, and building towards efficiency and more sophisticated models. In-the-moment data allows teachers to move students more quickly than using only interim assessments or exit tickets.
Resources
1 Mercer, Neil (2006). Teaching Children How to Use Language to Solve Math Problems.
2 Bambrick-Santoyo, Paul (2016). Get Better Faster: A 90-Day Plan for Coaching New Teachers.
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


