Por Steph Primiani, Director de STEM y Alicia Cuomo, Universidad de Brown Intern Política de Educación Urbana
El viaje
Al inicio de la 2018-19 año escolar, Blackstone Valley Prep puso en marcha un proyecto piloto en sus aulas de 5º grado de un bloque de instrucción diaria de 20 minutos dedicados a la solución de problemas de la historia fracción, llamados Historias de matemáticas. Sobre la base de un enfoque conceptual a problemas de la historia creada por Logro en primer lugar 2014-15 y los materiales de las escuelas FirstLine en Nueva Orleans, Historias de matemáticas trabaja en conjunto con el plan de estudios de matemáticas de BVP.
El piloto fue en respuesta a algunas cosas…
- Las normas de la fracción básico común de matemáticas para los estudiantes llaman a representar y justificar las ideas conceptualmente. sin embargo, muchos profesores se les enseñó fracciones utilizando el memorización de los procedimientos.
- la investigación sugiere que la educación comprensión conceptual de las fracciones es la base de los conceptos más abstractos. “Comprensión de las fracciones elementales es el más fuerte predictor de éxito en Álgebra 1” (Siegler et al, 2012).
- Comisionado de Educación de Rhode Island Ken Wagner directamente atribuida falta de avances en las puntuaciones de matemáticas PARCC a “un problema con fracciones.”
En el pasado 15 memos, hemos explorado el impacto que las historias de matemáticas plan de estudios ha tenido en los profesores y estudiantes de 5º grado en las escuelas Blackstone Valley Prep. Este último post del blog resume la amplitud de la investigación en educación que soporta la estructura de las plantas de matemáticas y destaca las prácticas de aula más transformadoras. En otras palabras: ¿Por qué es importante la aproximación? ¿Qué estrategias podría maestros considere la adopción para apoyar la comprensión conceptual de los estudiantes de las fracciones?
¿Por qué es importante la aproximación?
El protocolo estructurado se convierte en una habilidad de por vida en la forma de resolver los problemas de matemáticas.
Cada Historias lección de matemáticas sigue el mismo protocolo:
- Visualizar: Los estudiantes a visualizar el problema historia.
- Modelo: Los estudiantes escriben la información, modelo, y resolver.
- Turn-and-Talk: En las asociaciones de habilidad mixta, los estudiantes se turnan para usar su modelo para explicar y justificar su razonamiento.
- mientras tanto, el maestro monitoriza de forma agresiva student / trabajo y recoge datos en-el-momento.
- estudiante seleccionado(s) compartir su modelo con la clase y explicar su razonamiento.
- Turn-and-Talk: Los estudiantes responden a una pregunta de discusión específica sobre el modelo.
- Discusión de la clase entera: Los estudiantes se basan en la comprensión de los demás por discutir la cuestión específica.
- Los estudiantes revisar su trabajo para representar nueva comprensión.
En el comienzo del año escolar, profesores dedican tiempo a enseñar el protocolo y explicar por qué cada paso es importante para los estudiantes. Por ejemplo, Si los estudiantes no conocen la importancia de la visualización, podrían precipitarse para calcular una respuesta. Pero, una vez que los estudiantes han convertido invertido y familiarizado con el proceso, tiempo valioso se guarda en dar instrucciones. Los estudiantes son menos centrado en las direcciones recordar y más centrado en hacer los cálculos. Promover, estos pasos son los mismos tanto si eres un estudiante de kindergarten o un adulto de la mano de obra. Ser capaz de visualizar, modelo, resolver, Y si hablamos de un problema de matemáticas en el contexto de toda la vida es una habilidad.
Los estudiantes se benefician de buceo de profundidad en un problema rigurosa.
El plan de estudios de matemáticas Historias presenta un problema de palabras por lección, acerca de 10-13 problemas al mes. Esto da a los maestros la flexibilidad de volver a examinar los tipos de problemas difíciles. Adicionalmente, los problemas se acumulan en el rigor. El rigor no significa más duro. Núcleo común define el rigor en matemáticas como un trípode equilibrado de la comprensión conceptual sólida, habilidad y fluidez procedimental, y la aplicación de habilidades en situaciones de resolución de problemas.
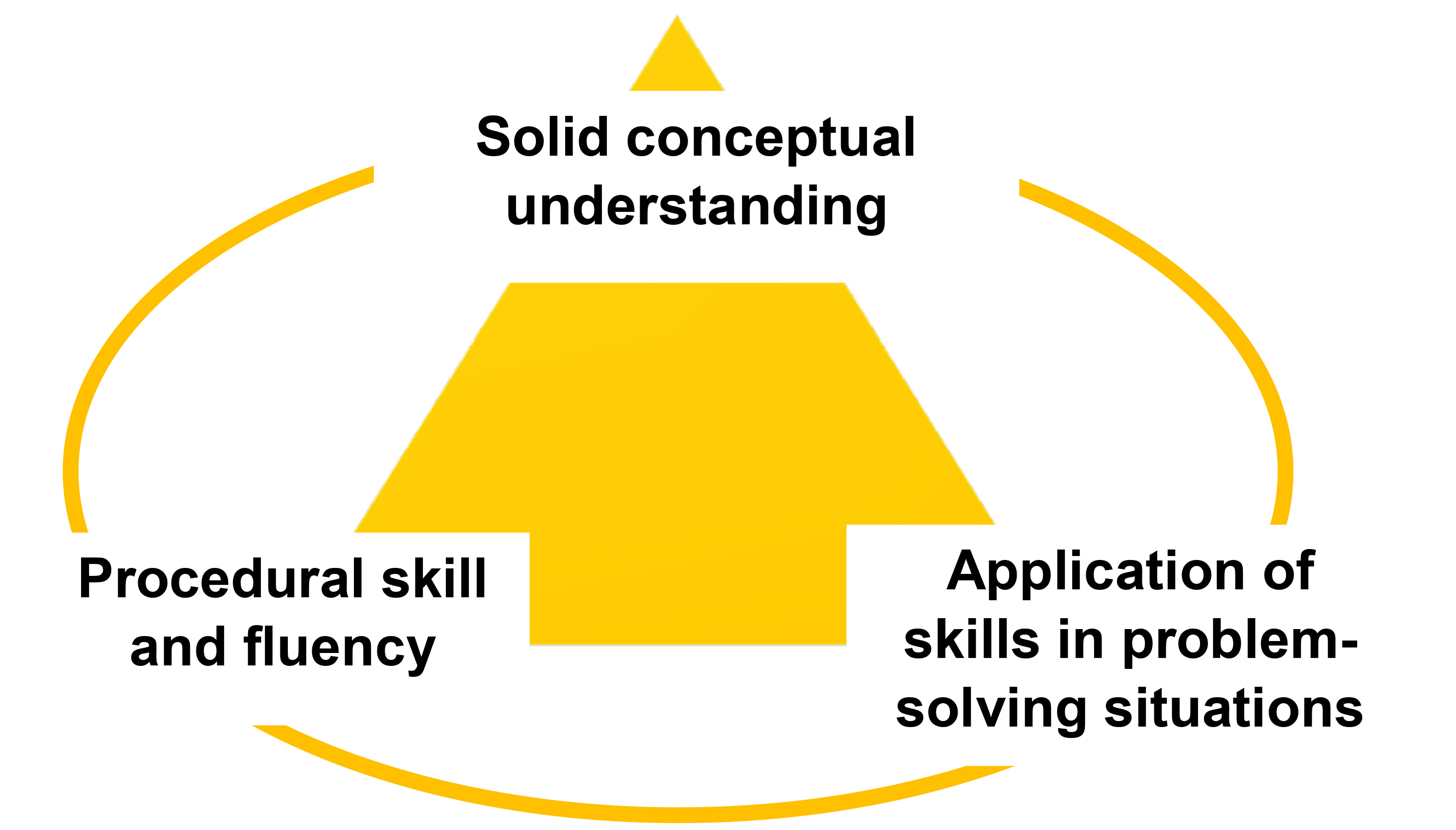
Durante Historias de matemáticas, estudiantes están pensando profundamente sobre un solo problema. Modelan el problema de forma individual con la intención de compartir sus ideas con un compañero y en última instancia la clase. Reexaminando un solo problema con múltiples modelos de muchas perspectivas, los estudiantes a desarrollar una comprensión conceptual más profundo de los conceptos.
Cuando los problemas de matemáticas están en contexto, mejor a los estudiantes pueden transferir fracciones conocimiento para escenarios realistas.
Cuando los maestros enseñan conceptos de fracciones en el contexto de un problema de la vida real, que ayudan a los estudiantes a visualizar el escenario y crean un contraste de modelos. Podemos imaginar fácilmente ¼ como una rebanada de pizza, longitud de la cinta, o un cubo de pintura, que se presta a aprender a dibujar múltiples representaciones simbólicas de esta fracción. También enseña a los estudiantes que las matemáticas se trata de la construcción de sentido y solución de problemas de la vida real.
Los estudiantes practican sensemaking, en lugar de memorizar los procedimientos, resolver problemas.
Muchos adultos en la U.S. fracciones que aprendió a través de un método tradicional son a menudo frustrados si no pueden recordar un procedimiento memorizado. Durante Historias de matemáticas, los estudiantes están descubriendo patrones y algoritmos por resolviendo problemas, en lugar de los patrones y algoritmos de aprendizaje a resolver problemas. "Con un basado en problemas abordar el estudiante tiene a quién recurrir aparte de sus propias ideas en relación con el problema. Como resultado, en lugar de buscar reglas, estudiantes intentan dar sentido a las ideas relevantes incrustadas en el problema o tarea” (Van de Walle, 2006). Los estudiantes que se enseñan con un enfoque como Historias de matemáticas tienen más resolución cuando se enfrentan a un problema complicado.
3 Estrategias de estudiantes basada en poner de relieve
El auto-monitoreo
Ellos no se den cuenta, pero solucionadores de problemas competentes no tenga prisa sin pensar. Hacen una pausa después de cada paso y se preguntan todo tipo de cuestiones internas como: ¿Qué información de la pregunta es importante?, ¿Cuál es el problema pidiendo?, y ¿Esta solución tiene sentido? Cuando los estudiantes piensan acerca de su forma de pensar, se dan cuenta de los patrones y construir una comprensión más profunda. Aquí hay algunas indicaciones para que los maestros modelo de auto-monitoreo.
Usando una variedad de modelos
Cuando los estudiantes modelar una solución más de una forma, tienen una comprensión más profunda de los conceptos de fracciones. METROHistorias ath apoya a los estudiantes en el aprendizaje de nuevas estrategias de sus pares. Aquí se presenta una ejemplo de tres enfoques distintos para el mismo problema historia.
Enseñanza en parejas
La investigación muestra que aprendemos pensar más cuando estamos guiando de otra persona porque las habilidades como aclaración de la información y la generación de preguntas requieren procesos mentales de alto nivel (Duran, 2016).
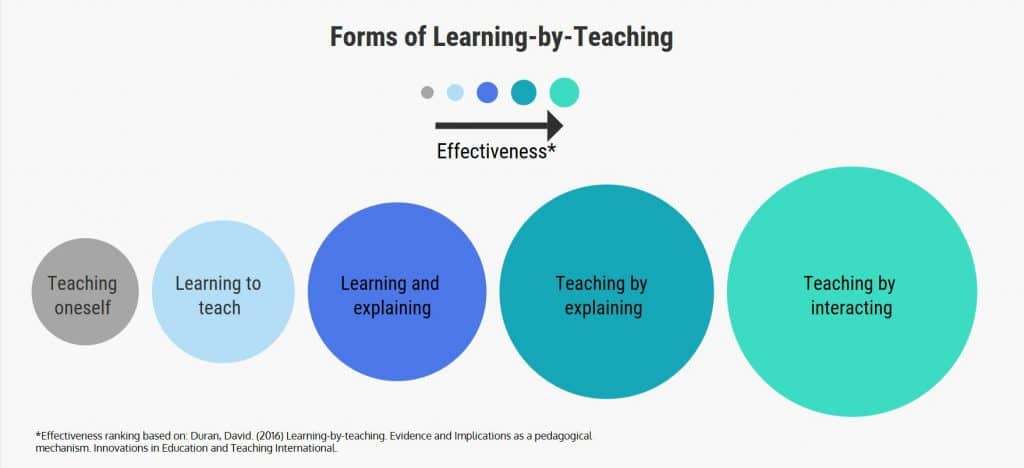
Mediante el uso de soportes como socios a su vez-y-habla y modelos visuales, los estudiantes pueden explicar su propio razonamiento, construir argumentos, e incluso identificar lagunas en la comprensión. Cuando los estudiantes interactúan, tienen una comprensión más profunda de los conceptos matemáticos.
3 Estrategias profesor-base para resaltar
Preparar haciendo el trabajo
Para prepararse para Historias de matemáticas, profesores resolver cada problema historia sí mismos y siguen una 4-Protocolo plan de lecciones paso.
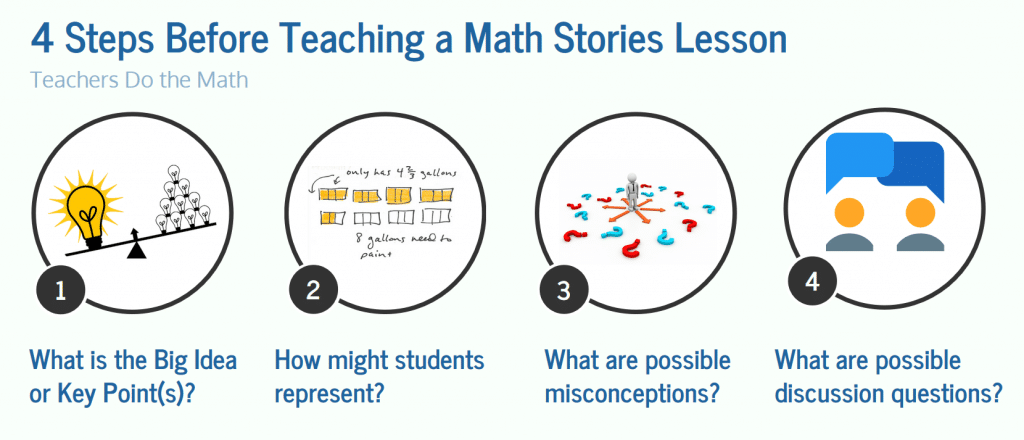
Al resolver los problemas de la historia de antemano, maestros internalizan los conceptos clave y pueden centrarse en facilitar y vigilar durante la lección. Esta preparación es especialmente crítico con los conceptos de fracciones, como muchos adultos se les enseñó métodos memorísticos y tradicionales están viendo básicos comunes estrategias conceptuales por primera vez como maestros.
Deje que los alumnos cometen errores
asuntos de mentalidad en las aulas de matemáticas. Aprendemos de nuestros errores, pero los estudiantes pueden olvidar rápidamente si esta comprensión rápida está ligado a altos grados de apuestas, o sentimientos de competencia en la clase. Por esta razón, es fundamental para que los maestros discuten abiertamente mentalidad de crecimiento con los estudiantes. aquí es un ejemplo de cómo discutir una idea errónea de que una clase puede conducir a una mayor comprensión.
No tenga miedo para asignar socios largos, historia de los problemas difíciles y celebrar la perseverancia. Pruebe con actividades problemas sin cola de la historia que están perdiendo la información clave y empujar a los estudiantes a hacer preguntas en lugar de encontrar respuestas.
En el apalancamiento del momento de Datos
Usando un rastreador de datos para registrar las observaciones del trabajo de los estudiantes y de la conversación ayuda a los maestros responden a lo que está sucediendo realmente en el aula. Rastreadores ayudan a los maestros hacen noticings objetivos acerca de las tendencias en el entendimiento que informan a la discusión y las próximas lecciones. aquí son algunos ejemplos de los seguidores de datos utilizados en la toma de decisiones durante Historias de matemáticas.
En suma
Está claro que el poder de las historias de matemáticas se encuentra en más de una secuencia de problemas de historias basadas en estándares andamiaje. Los maestros están implementando un protocolo que anima a los estudiantes a aprender mediante el modelado, la resolución, e interactuar con sus pares de todo los problemas contextuales. Promover, los estudiantes son más propensos a mantenerse motivados y comprometidos, ya que están discutiendo el trabajo producido desde dentro de la clase. Un marcador de un plan de estudios de la calidad es que enseña a los maestros, y las prácticas pedagógicas incrustados en las historias de matemáticas están sólidamente apoyados por educadores e investigadores. Como graduado de grado quinto de este año, BVP espera examinar cómo este nuevo enfoque seguirá marcando el conocimiento conceptual de los alumnos y las actitudes hacia las matemáticas.
Tener preguntas? Llegar a Director de STEM BVP, Steph Primiani en sprimiani@blackstonevalleyprep.org y sígueme en Twitter @stephprimiani


