By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern

Making Mistakes

How do you feel when you make a mistake?

Do your cheeks flush? Do you feel a weight in the pit of your stomach? Do you want to give up?

The neurological word for this response is ERN or error-related negativity, and it’s how brain synapses fire when you make an error or fail a task. Luckily, our brains (and the brains of all primates) are also equipped with an error-related positivity response, or Pe, that swiftly follows when enacted. Pe drives us to process, monitor, and correct errors instead of accepting defeat.¹

 

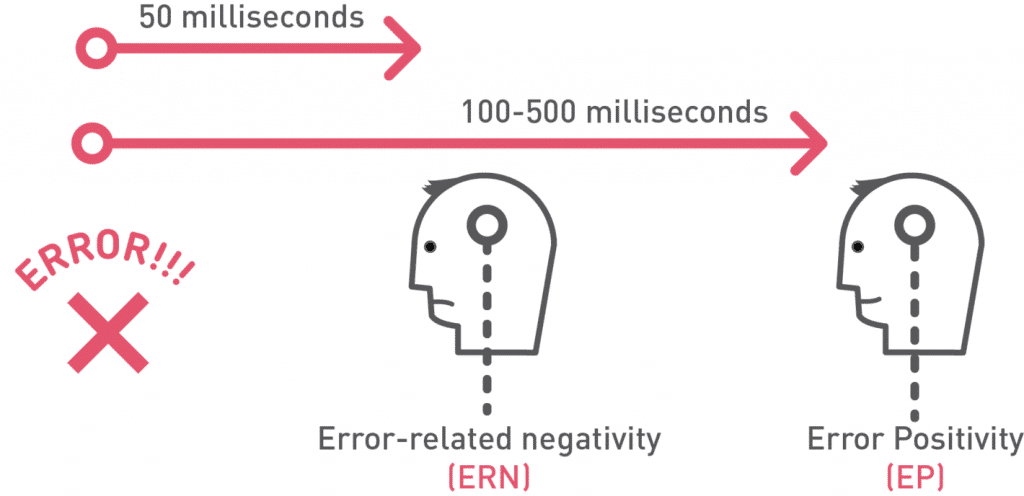2

 

What is most compelling about the neurological findings of Moser and other 21st century researchers is that the amplitude of a person’s ERN and Pe is malleable. In other words, how you respond to failure is a skill that can be grown.

 

Two Mindsets

“Whether you think you can or think you can’t–you are right.” – Henry Ford

The idea that we can strengthen and grow the ERN and Pe receptors closely aligns with psychological research on growth and fixed mindsets. Stanford University psychologist Carol Dweck studied thousands of students over three decades to answer questions about how attitudes and beliefs towards learning affect achievement. At the core of her findings is the existence of two polar learning mindsets. A fixed mindset perceives intelligence as static, whereas a growth mindset perceives intelligence as developed.

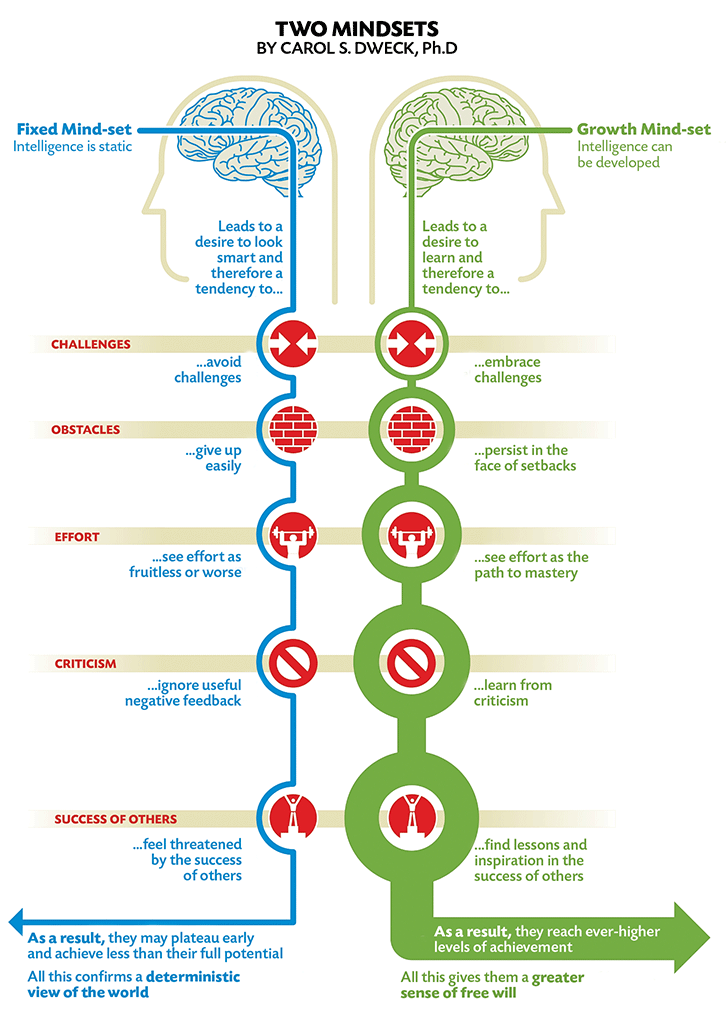
When teachers and administrators actively work to cultivate a growth mindset culture, students see mistakes as opportunities to learn rather than a frustrating reflection of their own innate ability, or inability. It’s important for teachers to talk to their students about the necessity of struggle in mathematics. When the brain is challenged, it grows–literally.

 

An Example in Action

Math Stories has a specific protocol for responding to student misconceptions.

Let’s consider the following story problem:

3 friends want to do a 4-mile relay race. They each need to run the same amount. How many miles should each friend run?

Student 1 and Student 2 solve independently using different models to represent their thinking…

Student 1

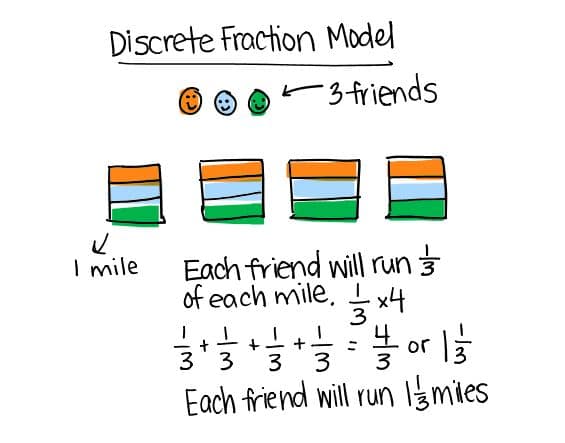
Strategy:

Student draws and labels the three friends. They draw four boxes to represent the four miles. They partition each mile into thirds because each of the three friends ran the same amount. ⅓ + ⅓ + ⅓ + ⅓ = 4/3 or 1 ⅓. Each friend ran 1 ⅓ miles.

---

Student 2

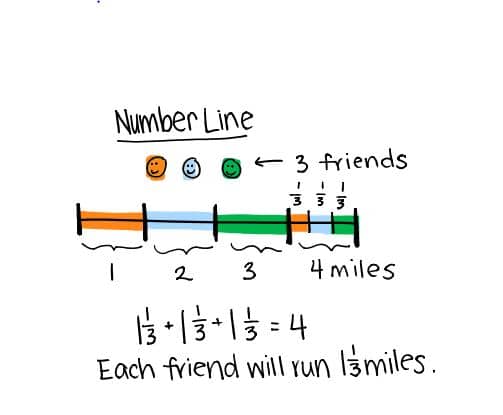
Strategy:

Student draws and labels the three friends. They draw a number line that extends to 4 to represent the 4 miles. Each friend runs an equal amount of miles, so each friend can run 1 mile plus some. Student divides the remaining mile into thirds. Each friend runs 1 ⅓ miles.

---

A common misconception is that students will reverse the operation…

Student 3

Strategy:

Student divides the number of friends, 3, by the number of miles, 4. Each friend runs ¾ miles.

While students are solving, the teacher is monitoring aggressively. Using a data tracker, the teacher records how individual students are solving and can quickly gauge what percent of the class modeled and solved correctly. If more than half of the class models and solves incorrectly, the Math Stories protocol guides teachers to lead a discussion about the common misconception.

In the example of the relay race problem, if more than half of the class incorrectly models ¾ as the solution, the teacher will show student work with the correct solution, 1 ⅓, alongside student work modeling the misconception, ¾ , and ask the following turn-and-talk question: Which of these solutions is reasonable? Why?

What is the advantage of having the class discuss Student 3’s misconception?

 

Reasoning with a Misconception

By discussing whether 1 ⅓ or ¾ is a reasonable solution with a partner, students are flexing important reasoning and communication skills. A possible exemplar response that teachers hunt for to highlight in the discussion may be:

Student 3 divided the number of friends, 3, by the number of miles, 4. Each friend runs ¾ miles. This cannot be correct because we know from the story problem that the number of friends (3), is less than the number of miles (4). So, we know that each friend will have to run more than a mile to get a total of 4 miles. ¾ is too small to be reasonable.

By assessing the validity of Student 3’s mistake, students are revisiting the language of the problem and visualizing the context to estimate an answer. This is the kind of sense-making that we want students to exercise not only during Math Stories, but in all real-life applications.

 

Cultivating a Positive Risk Culture

This kind of discussion driven by authentic mistakes is only possible in a class where students have a growth mindset and errors are a pathway to higher learning.

Teachers are constantly sending students spoken and tacit messages about their ability to learn. Researcher Jo Boaler suggests that teachers pay greater attention to how they’re communicating a growth mindset to students in the following areas:

 

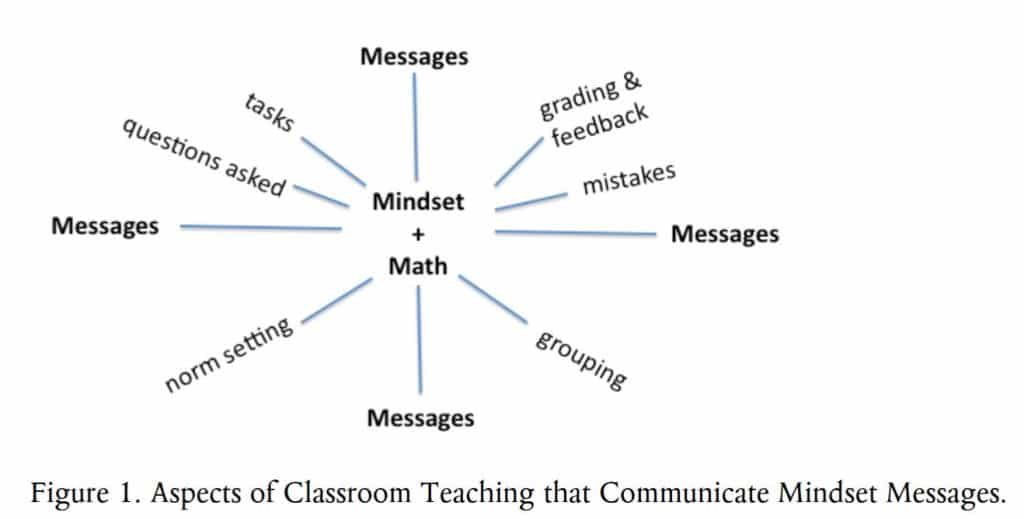
We can use Boaler’s evidence-based domains to generate a list of recommendations for teaching students to view mathematics with a growth mindset:

• Give students opportunities to struggle with long, challenging story problems.
• Set norms with students by explicitly naming mistakes as opportunities for growth.
• Reward perseverance and grit rather than “intelligence.”
• Place students in heterogeneous mixed-ability groupings.
• Teach students about brain plasticity and celebrate growth rather than grades.
• Ask students to justify their reasoning, both when they’re correct and incorrect.

Boaler’s research suggests that it’s important for teachers to ask students to justify their reasoning even when they’re correct. This habit teaches students to reflect on their solution and practice sense-making independently– not as a reflex when an error is discovered.

Mistakes are opportunities to learn and think deeply. Instead of grading with a punitive red x, Boaler suggests you may even try a star. Before using student work to highlight a misconception, ask permission from the scholar and make known that it will help the whole class grow.

Students perform better when they have explicit conversations with their teachers about perseverance and the importance of making mistakes. Class Dojo and Stanford’s PERTS Research Center collaborated to create a 5-part animated video series called The Mojo Show for educators and parents to teach young students about growth mindset. It’s a free tool with linked discussion questions and activities.

Another of Boaler’s major findings is that grouping practices perpetuate a fixed mindset belief among teachers and students. Students are placed in ability-based groupings with greater prevalence in the U.S. and England compared to high-performing countries like Japan and China. Further, much research has shown that although teachers believe they are giving more “appropriate” work to students placed in low groups, it is often not demanding enough (Blatchford et al.). Students may be receiving remedial instruction or “double dipping” during a different time of day to fill academic gaps, but Math Stories is an opportunity for students to learn from mistakes and to achieve at high levels… because they can.

 

Resources

¹ Moser, et. al. (2011) Mind Your Errors: Evidence for a Neural Mechanism Linking Growth Mind-Set to Adaptive Posterror Adjustments.

² Caviglioli, Oliver. (2015) Errors.

³ Boaler, Jo.The Mathematics of Hope: Moving from Performance to Learning in Mathematics Classrooms.

⁴ Steuer et al. A constructive error climate as an element of effective learning environments.

⁵ Boaler, Jo. (2013) Ability and Mathematics: the mindset revolution that is reshaping education.

 

Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani