By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
“Have you ever talked to yourself about math in the mirror?”
It may seem like a stretch, but research shows that when we explain things aloud–whether to ourselves, a passive audience, or better yet, another human being, we learn better.
A Paradigm Shift in Learning Theory
In the mid-90s, a famous article titled From Teaching to Learning was published, and it’s still referenced and read by many entering the Education sector. Authors Barr and Tagg described American classrooms dominated by an instruction paradigm in which the focus is on how instruction is delivered, students are sorted, and teachers are content experts who primarily lecture. They describe a necessary shift in mentality to a learning paradigm in which the focus is student-centered, knowledge is built rather than delivered, and teachers act as facilitators within a collaborative, supportive environment.
The Learning Paradigm frames learning holistically, recognizing that the chief agent in the process is the learner. Thus, students must be active discoverers and constructors of their own knowledge. In the Learning Paradigm, knowledge consists of frameworks or wholes that are created or constructed by the learner. Knowledge is not seen as cumulative and linear, like a wall of bricks, but as a nesting and interacting of frameworks. Learning is revealed when those frameworks are used to understand and act. Seeing the whole of something-the forest rather than the trees, the image of the newspaper photo rather than its dots- gives meaning to its elements, and that whole becomes more than a sum of component parts. Wholes and frameworks can come in a moment-a flash of insight-often after much hard work with the pieces, as when one suddenly knows how to ride a bicycle.1
Nearly thirty years later, just how student-centered a school’s philosophy and curriculum design is certainly varies, but by and large the United States is moving away from a banking system and towards frameworks that give students agency.
How does Math Stories create a student-centered learning environment? What supplemental classroom practices support students learning by teaching?
Building Knowledge
How do educators build knowledge in mathematics rather than tell knowledge in lectures? The Math Stories protocol intentionally uses cooperative learning methods so that ideas come from students.
In a past blog post, I described the 5-step Math Stories protocol:

The protocol is straightforward for teachers to follow and focuses on one daily story problem, enabling students to deep dive into concepts rather than skirt the surface. Although only about 20 minutes long, the theory behind the structure is that each step builds on individual understanding, culminating in a whole class discussion that stamps some key point or misconception that the observed student work from minutes earlier deems relevant. One way that Math Stories builds understanding is by allowing students to learn by teaching using cooperative strategies.
In 2016, researcher David Duran reviewed half a century of scientific articles written about the effects of learning by teaching. Within Duran’s framework, when we learn something knowing that we will teach it, we learn more effectively than when we learn for ourselves. This is because we’re using different mental processes when we revise and organize material to present it to someone else.
When we are responsible for explaining concepts to another individual, we learn even better because we have opportunities to clarify information, argue, and recognize gaps.
Finally, when we teach by interacting, generating questions and trying to guide another individual’s thinking, we learn the most.
Students benefit from a blend of learning-by-teaching methods, but it’s useful to see the progression:
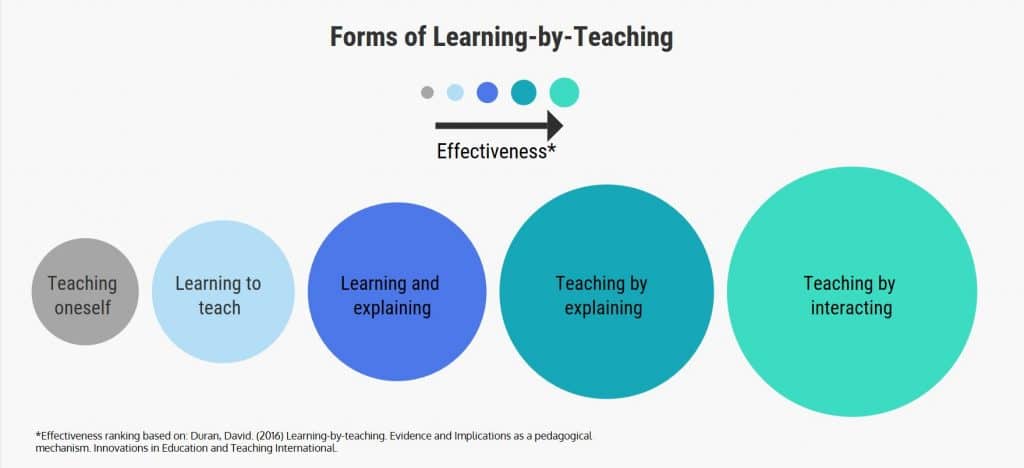
Instead of as a series of steps, we can also examine the Math Stories protocol as a ladder students climb as they learn by teaching:
When they are creating a model…

students are aware that they will be using their labeled representation to explain to their partner how they interpreted the story problem and solved.
During turn-and-talks…
students take turns explaining how they solved using their labeled models. If students are taught to point out gaps and ask challenging questions, this becomes teaching by explaining.
In the discussion…

he teacher strategically chooses students to share their work and explain their thinking to the class. This is learning and explaining. When students engage in a turn-and-talk about the share, they may raise clarifying questions or disagreements.
It may take time and patience to create mixed ability partnerships that also function on a social level, but it’s worth the investment. Not only do students learn better when they’re explaining their thinking to a peer or teaching them a new strategy they used, but this is realistic preparation for collaborating in higher education and their future careers. Rarely do we work alone.
An Example in Action
Let’s consider the following story problem:
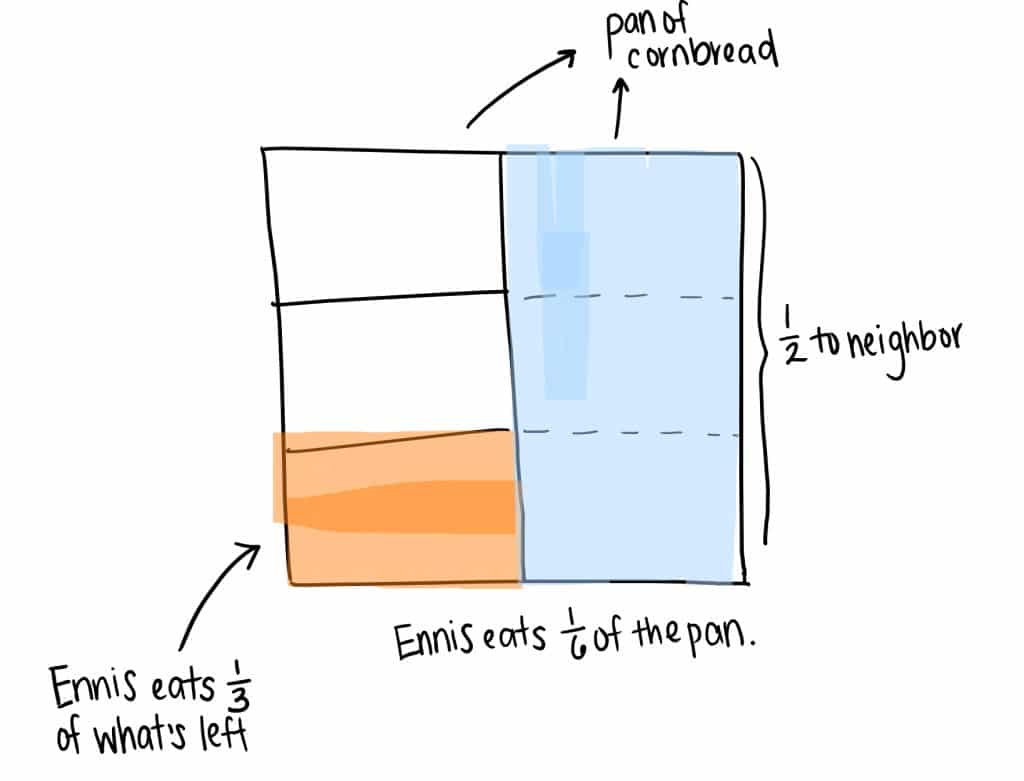
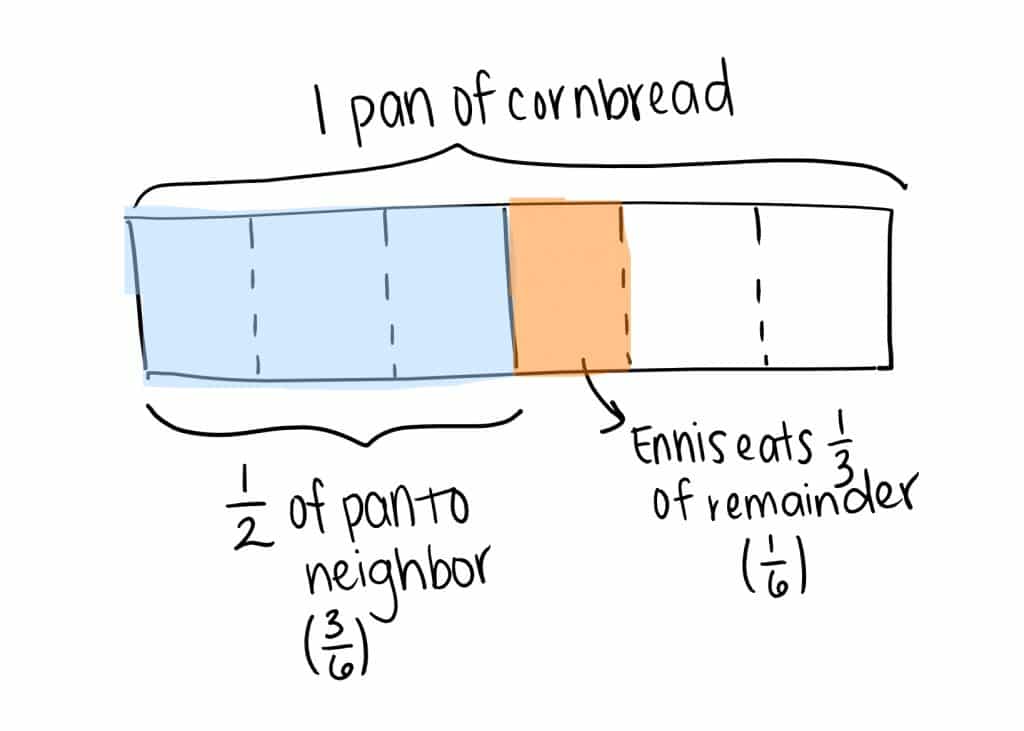
Ennis bakes a full pan of cornbread. Then he gives half of the pan of cornbread to his neighbor. After that, Ennis decides to eat ⅓ of the cornbread he has left. What fraction of the pan of cornbread did Ennis eat?
Within Math Stories, students know that they will be sharing their model and explaining their strategy to a partner. This is learning to teach in action. Students are more engaged because work isn’t being collected and returned the next day– they’re sharing and receiving feedback almost immediately. There’s also a rationale for including labels, a neat representation, and a clearly recorded solution.
Some students may solve like this:
Or like this:
But, a very common misconception is modeling ⅓ of the pan instead of ⅓ of the remainder after the neighbor eats ½:
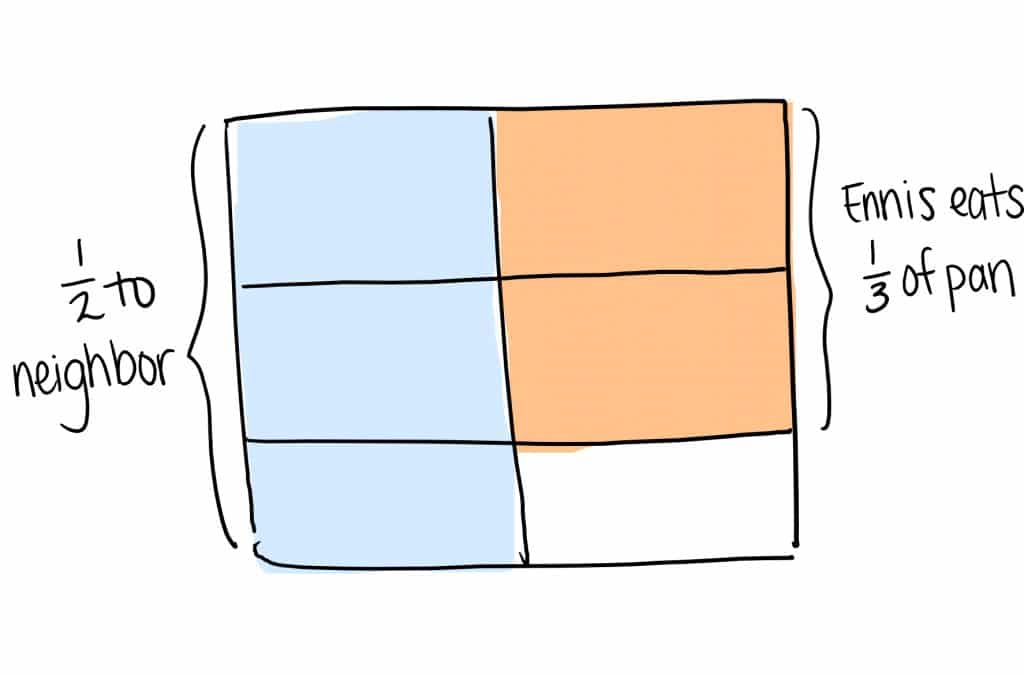
Another possible misconception is drawing the model correctly, but failing to partition the ½ Ennis gives his neighbor into thirds to create sixths. In this case, it appears that Ennis ate ¼ of the whole cornbread:
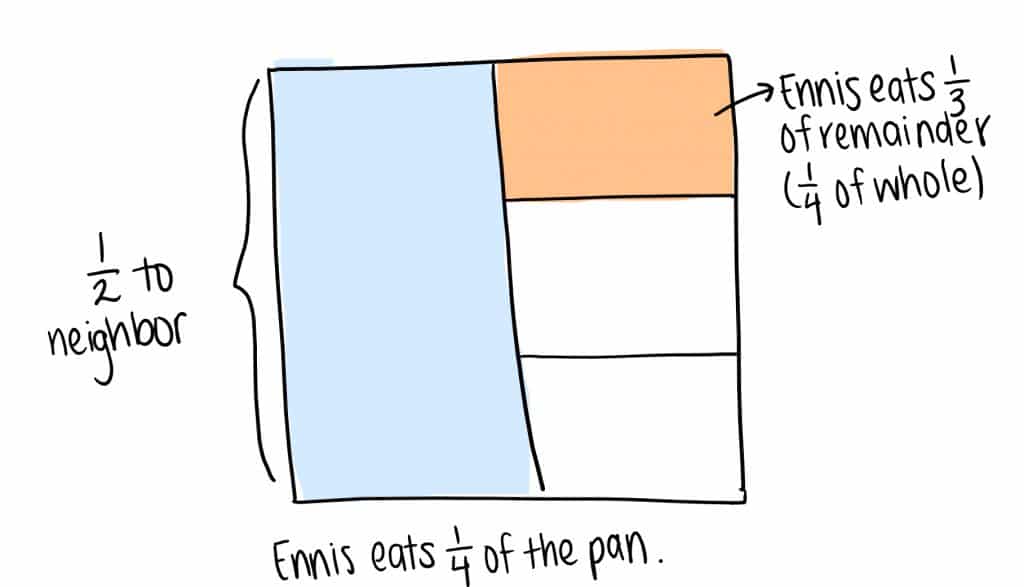
Misconceptions are a critical part of the learning process, but they become an issue when they’re not addressed. This leads to gaps in understanding. Within the Math Stories protocol, the turn-and-talk gives students the opportunity to talk through their strategy and solution to a peer who can point out misconceptions. This is learning and explaining and/or teaching by explaining in action. Students are more aware of the concept they’re explaining when they’re empathizing with a peer and trying to gage their understanding. Quite often students catch their own mistakes as they’re listening to themselves talk.
A second turn-and-talk during the discussion has the same benefits, but students are communicating about targeted student work. This is an important difference. It’s possible during the first turn-and-talk that both students are struggling with an incorrect answer. But, by circulating and using a tracker to identify class trends, the teacher has control over the model/strategy students are examining and the question they’re answering during the second turn-and-talk.
Further, the selected student(s) are teaching in the front of the classroom when they share their work. Students teaching is powerful. It livens up classrooms that are often dominated by teacher talk. Students practice communication skills, and it requires higher level skills to organize their thinking for an audience.
Supplemental Classroom Practices
Whether during Math Stories or other times in the school day, there are a variety of classroom practices that embody learning by teaching and all of its benefits:
Learning-by-teaching Strategies
Learning by developing educational materials. Students create materials (e.g. diagrams, physical models) to teach a peer.
Learning by replacing the teacher in front of the class. Students teach the class a concept or strategy.
Learning by co-teaching. Students teach the class a concept or strategy with the support of the teacher.
Learning by teaching through cooperative learning methods. The teacher assigns student roles or organizes students in diverse groups. For example, in jigsaw learning, students become an “expert’ in one facet of a topic by exploring provided materials and then join a group of other experts to share what they’ve learned. Other cooperative learning strategies are detailed here.
Learning by peer tutoring. A student who is more fluent in a concept teaches his/her peer.
Learning by peer assessment. Students correct/revise another student’s work and provide feedback.
Sage and Scribe
One of my favorite cooperative learning strategies is sage and scribe. In sage and scribe, students work in partnerships with one piece of paper. One student is the sage and one student is the scribe. The sage has access to the problem or task and their job is to describe it to the scribe, who is the only one who can write. Students switch roles and repeat the procedure for a new problem.

When sage and scribe is used in math instruction, students are teaching by interacting. They are guiding their partner in understanding and recording a correct solution.
The benefits are fruitful compared to traditional instruction. Students get immediate feedback from their partner, rather than having to wait for a teacher to circulate or grade work. Students learn social skills and teamwork in the context of a structured activity where what matters is communication. In classrooms where students are prone to forming cliques, sage and scribe gives students the opportunity to work with different types of learners. In classrooms where students are reluctant to raise their hands, this activity necessitates all students actively engaging and talking.
Finally, when students are communicating aloud about key concepts and strategies, they build critical metacognitive skills– thinking about their thinking.
Resources
1 Barr, Robert & Tagg, John. (1995) From Teaching to Learning–A New Paradigm for Undergraduate Education.
2 David Duran. (2016) Learning-by-teaching. Evidence and implications as a pedagogical mechanism. Innovations in Education and Teaching International.
3 Boud, et al. (2014) Peer Learning in Higher Education: Learning from and with Each Other.
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


