By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern
Which of these math problems makes more sense to you?
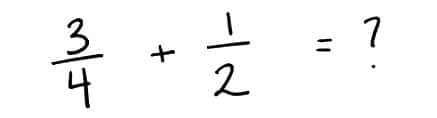
Combine 3/4 and 1/2.
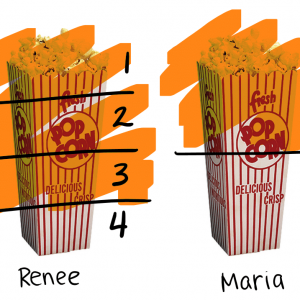
Renee eats 3/4 bag of popcorn. Then Maria eats 1/2 bag of popcorn. How much popcorn did Renee and Maria eat altogether?
Both problems require the same skill–finding equivalent fractions to combine two numbers with unlike denominators. But, the popcorn question provides a realistic context for why.
“Teaching through problem solving might be described as upside down from teaching for problem solving—with the problem(s) presented at the beginning of a lesson and skills emerging from working with the problem(s).”1
The narrative structure of the story problem question invites students to create a model with labels. Within a discrete fraction model, students partition to find the equivalent fraction:
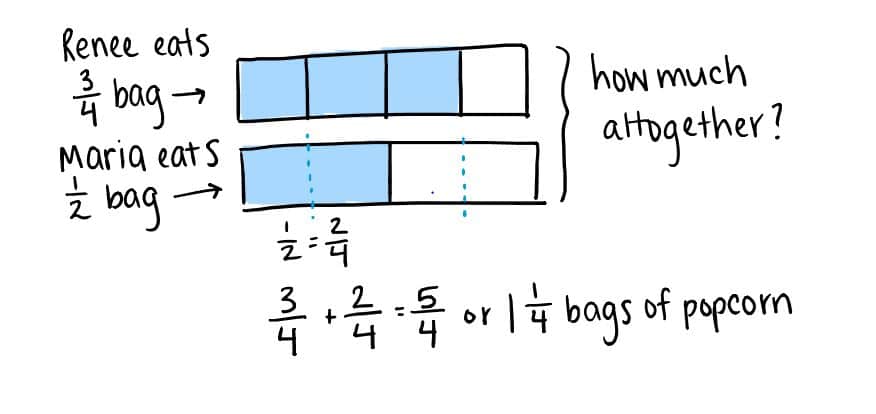
Within a number line model, the popcorn story is more explicitly visualized as a series of events, the last jump being the sum:
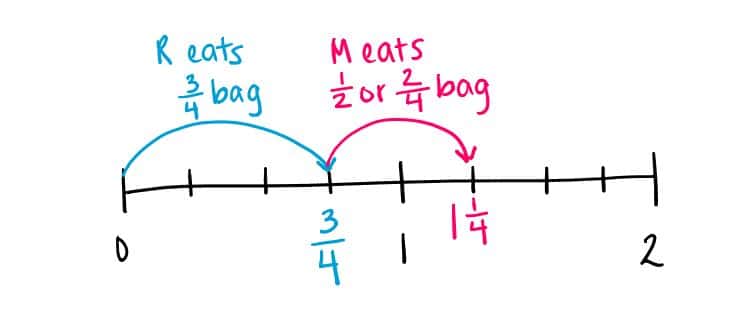
By creating a model to combine the portions of popcorn, students are guided to discover the procedure for finding equivalent fractions. Further, they immediately know one realistic context where a mathematical skill can be applied, and students can more easily notice patterns in problem types to use more efficient strategies and solve increasingly complex scenarios.
The Problem-Based Classroom
In a 2006 conversational interview, mathematics professor and author John A. Van de Walle stressed the need for all American classrooms to norm a problem-based approach led by the ideas of students rather than teacher-directed lecture. When the teacher is lecturing in a show-and-tell approach, Van de Walle argues that students are focused on the directions and rules rather than the mathematical concepts.
With a problem-based approach the student has nowhere else to turn other than his or her own ideas as they relate to the problem. As a result, rather than looking for rules, students attempt to make sense of the relevant ideas imbedded in the problem or task. Even if a problem is not solved, their own relevant ideas have been engaged. The class discussion that follows will be meaningful and interesting. Ideas are developed and integrated with each learner’s existing understanding.
For me it is also extremely important to consider what each approach is saying every day to students. With teacher-directed, wonderful explanations, students often view mathematics as a collection of rules that often become confusing and have little meaning… In the problem-based classroom students…experience the most basic fact of mathematics: math makes sense. Further, they come to realize that they are the ones who are capable of making sense of mathematics.1
The 20-minute Math Stories protocol is a student-centered approach that does just what Van de Walle suggests–forces students to independently make sense of challenging problems in realistic contexts. How can teachers leverage context in Math Stories and during their core instructional block? Why does context matter in a student-centered approach?
Non-Routine Problem Solving
Part of Van de Walle’s vision is that mathematics is not about being able to identify problem types and apply straightforward algorithms. Rather, problem solving in mathematics is non-routine.
Definitions of problem solving vary across curricula, but in essence they are non-routine questions that can be solved using more than one strategy. “Learning multiple strategies may help students see different ideas and approaches for solving problems and may enable students to think more flexibly when presented with a problem that does not have an obvious solution.”
The 5th grade Math Stories sequence has approximately 70 story problems. It is a carefully scaffolded progression that begins with a review of 4th grade concepts, then a couple months in, students move into 5th grade fraction standards using all four operations. There are generally 10-13 story problems a month, which gives teachers the flexibility to spiral challenging problem types and revisit concepts.
What’s key about the daily story problem is that it presents a mathematical challenge in context. Providing context is crucial to supporting students in sense-making and flexible problem solving. Further, story problems support students in developing skills in three areas RAND (a huge nonpartison research corporation) has deemed necessary for building proficiency:
- Representation
- Justification
- Generalization
Supporting Student Independence
Whereas students may be primed to identify the problem type in an explicit lesson and follow a familiar procedure, in Math Stories, students aren’t given any information in addition to the story problem. As Van de Walle suggests, this hands-off structure forces students to think about what information they already know and what they are being asked to solve for. Theoretically, this sounds great, but in classrooms students have varying needs, are still developing metacognitive skills, and are often quick to skim problems and rely on straightforward algorithms.
How do we train students to read story problems carefully?
The Checklist
A question list can support students in reading a story problem thoroughly for known and unknown information. The What Works Clearinghouse (WWC) is funded by the Institute of Education Science (IES) through the U.S. Department of Education and is a huge resource of education research. Here is WWC’s sample list of prompts:
Model Self-Monitoring and Reflection
Teachers should model how to use prompts like the ones listed above to reason with oneself throughout the problem solving process–when reading the story problem, choosing a strategy to solve, and checking your work. Students learn from example how to think aloud to themselves when solving a story problem. Here is an example from WWC, adapted to Math Stories, of a student self-monitoring. The student asks and answers a sequence of questions that’s the same no matter the problem type:
Example Problem
5 friends are planning on splitting 3 pizzas evenly. One of the friends can’t come to dinner anymore. How much more pizza will the friends get if only 4 people split the pizzas instead of 5 people splitting the pizzas?
Solution*
Student: First, I ask myself: “What is the story about, and what do I need to find out?” I see that the problem has given me the total amount of pizza and two different scenarios for sharing the total amount of pizza. I know that “how much more” is asking me to compare, or subtract, the difference between how much pizza each friend gets in each scenario.
I ask myself, “Have I seen a problem like this before?” As I think back to the story problems we’ve done, I remember seeing a problem where friends were sharing a pan of brownies. I remember we had to divide the whole by the number of friends to get each friend’s portion. This seems like a similar kind of problem, but I’m going to have to divide twice because there are two scenarios and then compare.
Before I go on, I ask myself, “What steps should I take to solve this problem?” It looks like I need to divide the total amount of pizza by the number of friends for each scenario.
4 friends: 3/5 pizza per person
5 friends: ¾ pizza per person
The problem is asking me “how much more” pizza the friends get when there are only 4 people splitting instead of 5. I know that when I’m comparing, or finding a difference, I can use subtraction. But, I have to have the same units to subtract.
I can use my model:

To write an equation:
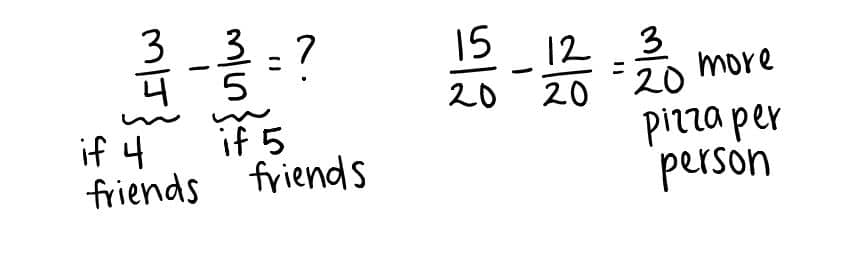
So, the difference is 3/20. The friends each get 3/20 more pizza when there are only 4 people compared to when there are 5.
Finally, I ask myself, “Does this answer make sense when I reread the problem?” It makes sense to me that 3/20 is the answer because it’s the difference between the portion size for 5 friends and 4 friends. 3/20 is a small number compared to the portion sizes. (I know 3/10 is the same as 0.3 or 3%, and 3/20 is even less!) This makes sense because the problem is asking me to find the difference—taking away 1 friend makes a small difference in how much pizza each person will get.
Support with Unfamiliar Language and Contexts
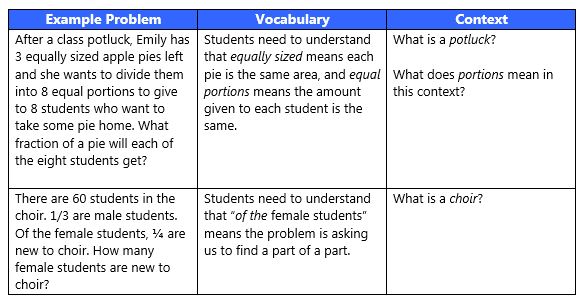
It is certainly true that students will encounter unfamiliar language and context on formal assessments that they will have to grapple with without the help of a teacher or peers. However, as WWC states: “The goal of ensuring that students understand the language and context of problems is not to make problems less challenging. Instead, it is to allow students to focus on the mathematics in the problem, rather than on the need to learn new background knowledge or language. The overarching point is that students should understand the problem and its context before attempting to solve it.” For this reason, it’s important for teachers to anticipate when the 5th graders in their class may need additional clarification, especially English language learners. Here is an example adapted from WWC using Math Stories story problems:
Personalize Story Problems
WWC and other research suggests students are more engaged and can make connections to the real life applications of math when story problems are personalized. Teachers should be careful not to do this all the time– students need to get used to thinking about scenarios outside of their comfort zone. But, sometimes including students’ names, beloved trends like beyblades, and having scholars come up with their own scenarios, can boost engagement. Each story problem in Math Stories is standards-based, so it’s simple to swap out the content for content that’s relevant to your classroom while still teaching key concepts.
Resources
1 (2006) A Conversation with John Van de Walle, author of Elementary and Middle School Mathematics: Teaching Developmentally.
2 RAND. (2003) Mathematical Proficiency for All Students: Toward a Strategic Research and Development Program in Mathematics Education.
Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani


