By Steph Primiani, Director of STEM and Alicia Cuomo, Brown University Urban Education Policy Intern

Hunting, Not Fishing

Have you ever cast a fishing line? The nature of fishing is that you never quite know exactly what you’ll get. Managing Director of the Uncommon Schools, Doug Lemov, remembers a leader at a workshop describing the power of choosing “hunting over fishing:”

The idea is that when you call on students and have no idea what they will say, that’s fishing. You hope you get a useful answer for discussion or analysis, but you don’t know what you’ll get. There’s nothing wrong with fishing–sometimes it’s nice to be surprised–but sometimes it can be better to hunt–to assign written reflection before discussion and to circulate during the discussion to choose specific students to call on to share because their answers will be most productive to discuss (often because they developed a key idea or made a common mistake everyone can learn from). It brings a whole new level of intentionality to discussions.¹

As hunters, teachers can stamp key mathematical points in a timely way, while still facilitating a discussion that’s centered around student ideas and student voice.

 

It’s All in the Protocol

Within the Math Stories protocol…

After solving the story problem using a representative model, students turn and talk with a partner to share their model using mathematical language and justify their reasoning. As students are sharing, the teacher is using a tracker to record how individual students are solving and quickly gauge what percent of the class modeled and solved correctly.

If most students are solving correctly, the teacher puts 2-3 models on the board from least to most sophisticated. The teacher asks partners to turn-and-talk in response to the following question: What makes these models the same or different?

This turn-and-talk is pivotal to the teacher, who is hunting for student responses he or she can use to craft a meaningful discussion.

In last week’s blog post, I spoke about teachers using a tracker to collect in-the-moment data, which then informs the discussion question they ask students. How can teachers listen in on partner talk and strategically use student responses to craft a discussion that builds student understanding?

 

In Context

Let’s consider the following story problem:

Lally brings 2/3 of a gallon of water to soccer practice. She was supposed to bring 1 1/2 gallons of water. How much extra water should she have brought?

Students must realize that you cannot add or subtract unlike denominators. They may use multiplication or partitioning to convert ⅔ to 4/6 and 1 ½ to 9/6.

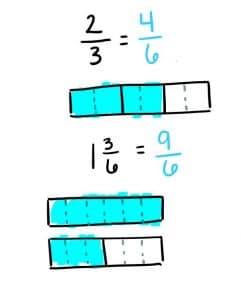
Students may draw a number bond to interpret the story problem:

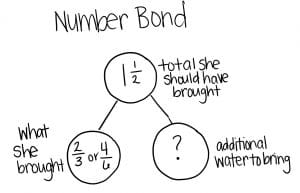
Number bonds help us see the inverse relationship between addition and subtraction. It supports students as they interpret the story using information from the problem.

We can tell the story two different ways:

Addition: The ⅔ water Lally already brought added to the extra water is equal to 1 ½ . The answer is how much added to ⅔ equals 1 ½ .

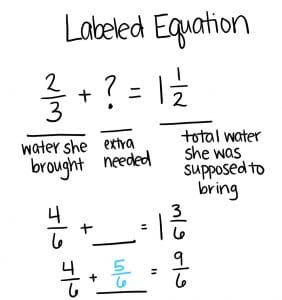
Subtraction: The 1 ½ total water Lally is supposed to have, take away the ⅔ water she already brought is equal to how much more she should have brought. The answer is the difference 1 ½ – ⅔.

By solving this problem, there are several key points that teachers may choose to stamp with students based on trends they’ve noticed in scholar work when scholars have worked on similar problem types:

Key Point 1

We need the same units to add or subtract numbers.

Key Point 2

We can use equivalent fractions to rewrite numbers with common units.

Key Point 3

The equation we write to model a situation might be different from the equation we think of to solve.

Key Point 3 asks for students to be flexible thinkers. Having students share out a variety of models helps them think deeply about relationships in math. If a teacher observes more than half of the class modeling correctly, she will choose 2-3 students with clear representations to share out how they solved at the board, then ask:

Student 1 represented the extra water with an addition equation. Student 2 represented the extra water with a subtraction equation. How can both be correct?

Students engage in a turn-and-talk with their partner in response to the discussion question. They point to the models on the board and use the language from the story problem to justify their reasoning. As students are talking, the teacher is listening in for students they can call on in an order that builds on understanding for the whole class.

What does this look like in the classroom during Math Stories?

 

An Example in Action

Let’s consider the following student models:

 

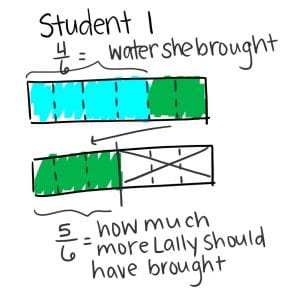
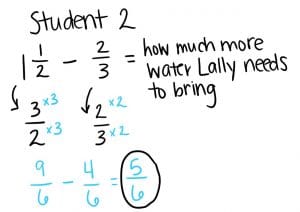
A scaffolded discussion with predetermined students to call on may sound something like this:

Teacher: __ can you start us off by sharing your interpretation of Student 1’s model?

Response 1: Student 1 drew all the water, that’s 1 ½ , then they divided the first gallon of water into ⅔ and partitioned it to make the equivalent fraction 4/6. They shaded the 4/6 and labeled it “water she brought.” Then they counted the unshaded sixths, stopping at a total of 1 ½ to get how much more Lally should have brought. They counted ⅚. Lally should have brought ⅚ gallons more water.

Teacher: __ can you share your interpretation of Student 2’s model with the class?

Response 2: Student 2 knew that Lally brought ⅔ of the total amount of 1 ½ , meaning that the difference is how much more she needs to bring. They multiplied to make fractions with like denominators and wrote an equation to subtract the numerators. 9 sixths minus 4 sixths is 5 sixths (⅚).

Teacher: If they used different strategies, how can they both be correct? __ can you share your response to the discussion question?

Response 3: Student 1 counted the sixths after 4/6 to find how much more Lally needed to add up to a total of 9/6. Student 2 used the inverse of this relationship, which is 9/6 minus 4/6. Whether you model it as addition or subtraction, you find the missing part, or the ⅚ that Lally should have brought.

 

After the third student responds to the discussion question, the teacher will affirm that this is correct and ask others to rephrase the key point in their own words or prove that the key point is true using a number bond. A true marker of excellence would be using the data tracker to intentionally call on students who modeled incorrectly. Are they now correctly interpreting the problem? Students will then all record the key point on their paper.

 

By listening in on turn and talk conversations (hunting), teachers can ensure the whole-class discussion is targeted and aligned to the key point. Had the teacher in the example fished by calling on raised hands, the discussion might have been muddled, resulting in fewer ‘aha’ moments and less likely enduring understanding.

 

What Does the Research Say?

The structure and pedagogy behind the 20-minute Math Stories protocol reflects America’s slow adoption of approaches to teaching mathematics that have proven successful in East Asian countries like China and Japan.

In the early 90s, a study of mathematics classes in 800 elementary schools across Beijing, China; Sendai, Japan; Taipei, Tawan; and Minneapolis and Chicago in the United States observed several trends in Chinese and Japanese classrooms that were less common in American schools:

• Presenting one mathematical concept in a variety of ways,
• The instructor performing as a coordinator rather than a judge,
• Providing concrete experiences before teaching abstract concepts, and
• Using techniques that facilitate conceptual understanding (Lee, 1998).²

The design of Math Stories addresses these areas that are often still overlooked in traditional core mathematics instruction in the U.S., and these practices create more actively involved learners.

When teachers use turn-and-talk responses to plan a scaffolded discussion, they’re acting as a coordinator. Further, they’re able to build on the entire class’ understanding by having students break down the problem and interpret a variety of models that increase in sophistication.

 

Resources

¹ Lemov, Doug. (2015) Hunting Versus Fishing.

² Fan, Lianghuo et al. (2004) How Chinese learn mathematics. Perspectives from insiders.

 

Have questions? Reach out to BVP’s Director of STEM, Steph Primiani at sprimiani@blackstonevalleyprep.org and follow me on Twitter @stephprimiani